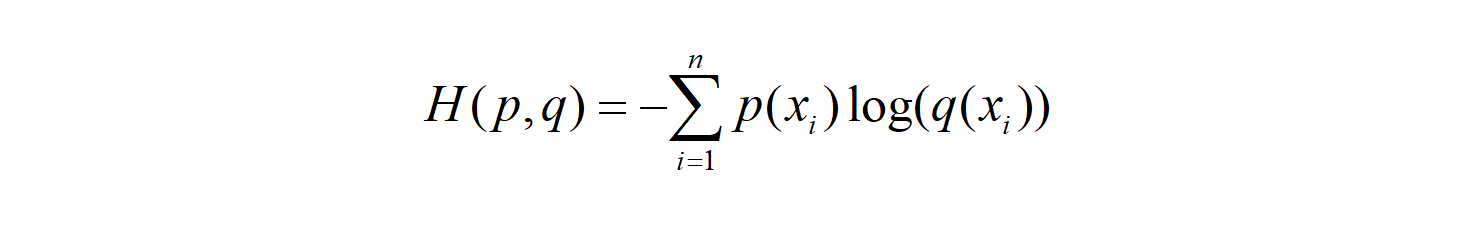Concept 1: Cross entropy
The amount of information
The amount of information in a message has a lot to do with its uncertainty. A sentence that requires a lot of external information to be certain is said to be informative. For example, if you hear “it’s snowing in xishuangbanna, yunnan”, you need to check the weather forecast, ask local people and so on (because it never snows in xishuangbanna, yunnan). On the contrary, if you are told that “people eat three meals a day”, the information of the message is very small, because the certainty of the message is very high.
Then we can define the information amount of event x0 as follows (where p(x0) represents the probability of event x0):
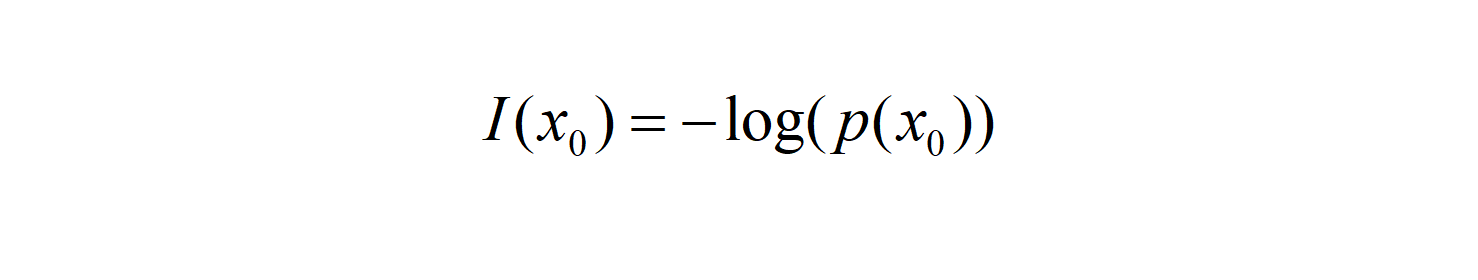
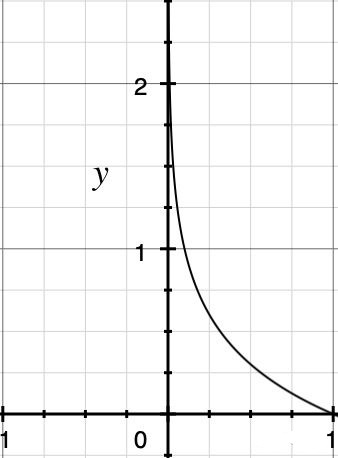
The probability is always between 0 and 1, -log(x) as shown above
Entropy
The amount of information is for a single event, but the reality is that a single event can happen in a number of ways. For example, a roll of dice can happen in six ways.Entropy is a measure of the uncertainty of a random variable, the amount of information expected from all possible events.The formula is as follows:
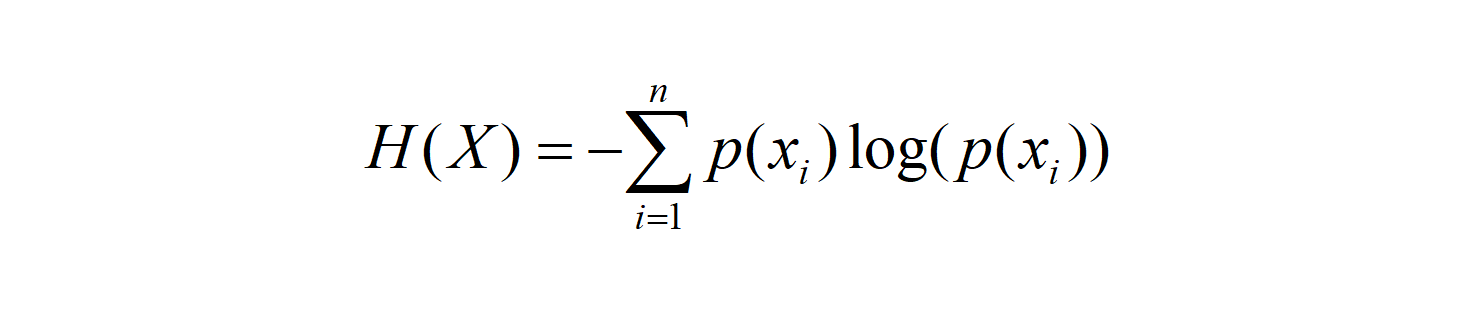
n represents the total number of situations in which an event is likely to occur
One of the special cases is the coin toss, in which there are only two cases (heads and tails). In this case (binomial distribution or 0-1 distribution), the entropy calculation can be simplified as follows:
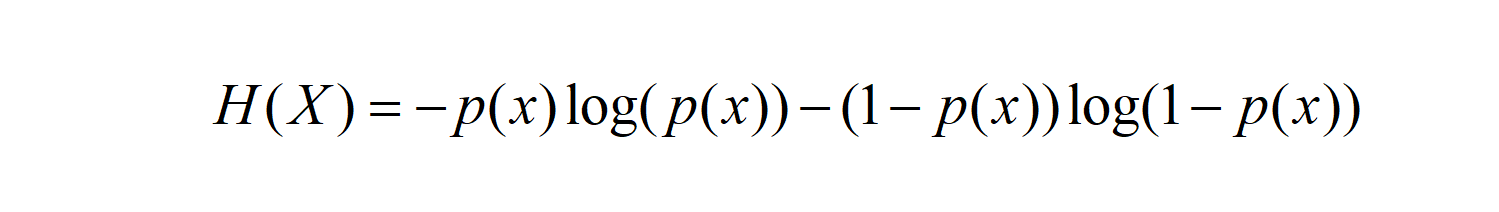
p(x) is the probability of heads,1-p(x) is the probability of tails (and vice versa)
Relative entropy
Relative entropy is also called KL divergence, it’s used to measure the difference between two distributions p(x) and q(x) for the same random variable x. In machine learning, p(x) is often used to describe the true distribution of samples, for example, [1,0,0,0] indicates that the samples belong to the first category, q(x) is often used to represent the predicted distribution, for example [0.7,0.1,0.1,0.1]. Obviously, using q(x) to describe a sample is not as accurate as using p(x), and q(x) requires constant learning to fit the exact distribution p(x).
The formula of KL divergence is as follows. The smaller the value of KL divergence is, the closer the two distributions are:
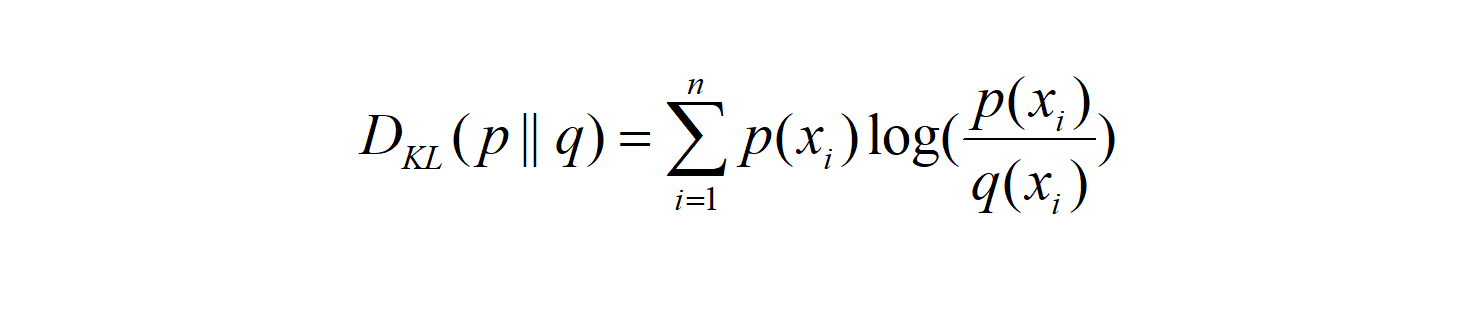
n represents the total number of situations in which an event is likely to occur
Cross entropy
We deform the formula of KL divergence and get:
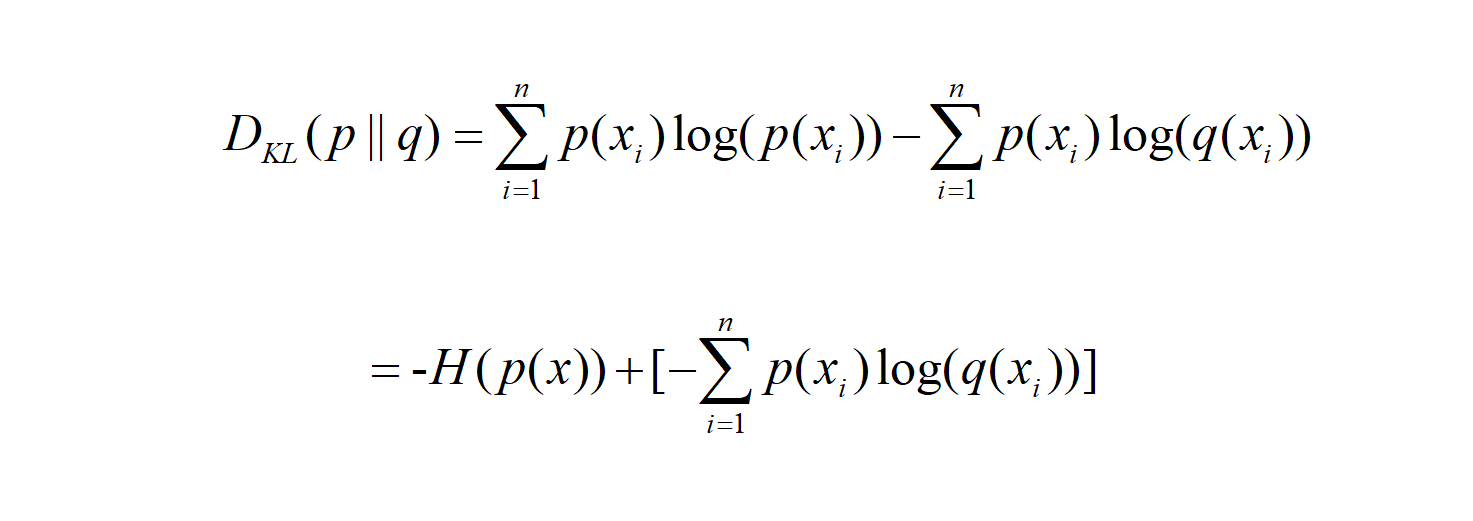
The first half is the entropy of p(x), and the second half is our cross entropy: