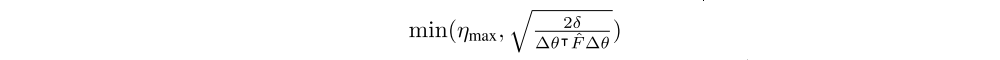Paper 3: Scalable Trust-Region Method for Deep Reinforcement Learning using Kronecker-Factored Approximation (ACKTR)

Slides

Abstract

We propose to apply trust region optimization to deep reinforcement learning using a recently proposed Kronecker-factored approximation to the curvature（曲率）.
We extend the framework of natural policy gradient and propose to optimize both the actor and the critic using Kronecker-factored approximate curvature (K-FAC) with trust region.
The first scalable trust region natural gradient method for actor-critic methods.
A method that learns non-trivial tasks in continuous control as well as discrete control policies directly from raw pixel inputs.

1 Introduction

The neural networks representing control policies in Deep RL methods are still trained using simple variants of stochastic gradient descent (SGD). `SGD and related first-order methods explore weight space inefficiently`. The distributed approach A3C was proposed to reduce training time by executing multiple agents to interact with the environment simultaneously, but this leads to rapidly `diminishing（削弱）returns of sample efficiency as the degree of parallelism increases`.

Sample efficiency is a dominant concern in RL. One way to effectively reduce the sample size is to use `more advanced optimization techniques for gradient updates`.

`Natural policy gradient` uses the technique of natural gradient descent to perform gradient updates. Natural gradient methods follow the `steepest descent（最速下降）direction that uses the Fisher metric as the underlying metric`, a metric that is based not on the choice of coordinates but rather on the manifold.

However, the exact computation of the natural gradient is intractable because it requires `inverting the Fisher information matrix`. TRPO avoids explicitly storing and inverting the Fisher matrix by using `Fisher-vector products`. However, it typically requires many steps of `conjugate gradient` to obtain a single parameter update, and accurately estimating the curvature requires a large number of samples in each batch; hence `TRPO is impractical for large models and suffers from sample inefficiency`.

`K-FAC is a scalable approximation to natural gradient`. It has been shown to speed up training of various state-of-the-art large-scale neural networks in supervised learning by using larger mini-batches. Unlike TRPO, each update is comparable in cost to an SGD update, and it `keeps a running average of curvature information`, allowing it to use small batches. This suggests that `applying K-FAC to policy optimization could improve the sample efficiency` of the current deep RL methods.

We introduce the `actor-critic using Kronecker-factored trust region (ACKTR)` method, a scalable trust-region optimization algorithm for actor-critic methods. The proposed algorithm uses a `Kronecker-factored approximation to natural policy gradient that allows the covariance matrix of the gradient to be inverted efficiently`. To best of our knowledge, we are also the `first to extend the natural policy gradient algorithm to optimize value functions via Gauss-Newton approximation`.

In practice, the per-update computation cost of ACKTR is `only 10% to 25% higher than SGD-based methods`. Empirically, we show that ACKTR substantially `improves both sample efficiency and the final performance` of the agent.

2 Background

2.1 Reinforcement learning and actor-critic methods

2.2 Natural gradient using Kronecker-factored approximation

To minimize a nonconvex function J(θ), the `method of steepest descent` calculates the update ∆θ that minimizes J(θ + ∆θ), subject to the constraint that ||∆θ||B < 1, where || · ||B is the norm defined by

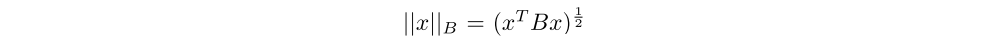
and `B is a positive semidefinite matrix（半正定矩阵）`. The solution to the constraint optimization problem has the form

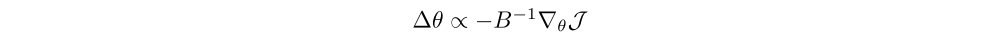
where ∇θJ is the standard gradient. When the norm is Euclidean, i.e., B = I, this becomes the commonly used method of gradient descent. However, the Euclidean norm of the change depends on the parameterization θ. This is not favorable because the `parameterization of the model is an arbitrary choice, and it should not affect the optimization trajectory`. The method of natural gradient constructs the norm using the `Fisher information matrix F, a local quadratic approximation to the KL divergence`. This norm is independent of the model parameterization θ on the class of probability distributions, providing a more stable and effective update. However, since modern neural networks may contain millions of parameters, `computing and storing the exact Fisher matrix and its inverse is impractical, so we have to resort to approximations`.

A recently proposed technique called `K-FAC uses a Kronecker-factored approximation to the Fisher matrix` to perform efficient approximate natural gradient updates. We let p(y|x) denote the output distribution of a neural network, and L = log p(y|x) denote the log-likelihood. Let W be the weight matrix in the ℓth layer. Denote the input activation vector to the layer as a, and the pre-activation vector for the next layer as s = Wa. Note that the `weight gradient` is given by

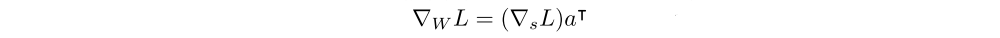
K-FAC utilizes this fact and further `approximates the block Fℓ (Fisher matrix) corresponding to layer ℓ as ˆFℓ`,

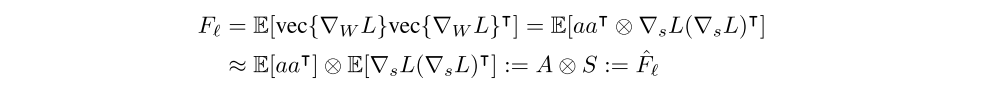
This approximation can be interpreted as making the assumption that the second-order statistics of the activations and the backpropagated derivatives are `uncorrelated`. By exploiting the `basic identities`

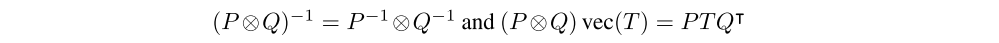
And with the above approximation, the `natural gradient update` can be efficiently computed

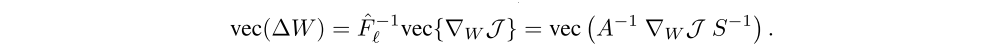
From the above equation we see that the K-FAC approximate natural gradient update only requires `computations on matrices comparable in size to W`. The K-FAC algorithm has been `extended to handle convolutional networks`.

3 Methods

3.1 Natural gradient in actor-critic

There still doesn’t exist a scalable, sample-efficient, and general-purpose instantiation of the natural policy gradient. In this section, we introduce the first scalable and sample-efficient natural gradient algorithm for actor-critic methods: the actor-critic using ACKTR method. `We use K-FAC approximation to compute the natural gradient update, and apply the natural gradient update to both the actor and the critic`.

To `define the Fisher metric` for reinforcement learning objectives, one natural choice is to use the policy function which defines a distribution over the action given the current state, and take the expectation over the trajectory distribution:

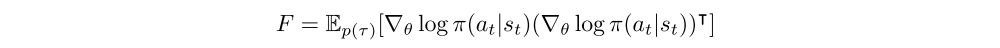
where p(τ) is the `distribution of trajectories`, given by

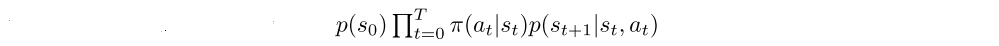
In practice, one approximates the intractable expectation over trajectories collected during training.

We now describe one way to `apply natural gradient to optimize the critic`. Learning the critic can be thought of as a least-squares function approximation problem, albeit one with a moving target. In the setting of least-squares function approximation, the second-order algorithm of choice is commonly Gauss-Newton, which `approximates the curvature as the Gauss-Newton matrix G := E[JTJ]`, where J is the Jacobian of the mapping from parameters to outputs. The Gauss-Newton matrix is equivalent to the Fisher matrix for a Gaussian observation model; this equivalence allows us to apply K-FAC to the critic as well. Specifically, we assume the output of the critic v is defined to be a Gaussian distribution p(v|st) ∼ N(v; V(st), σ2). `The Fisher matrix for the critic is defined with respect to this Gaussian output distribution`. In practice, we can simply set σ to 1, which is equivalent to the vanilla Gauss-Newton method.

If the actor and critic are disjoint, one can separately apply K-FAC updates to each using the metrics defined above. But to avoid instability in training, it is often beneficial to use an architecture where the two networks share lower-layer representations but have distinct output layers. In this case, we can `define the joint distribution of the policy and the value distribution` by assuming independence of the two output distributions, i.e., p(a, v|s) = π(a|s)p(v|s), and construct the Fisher metric with respect to p(a, v|s), which is no different than the standard K-FAC except that we need to sample the networks’ outputs independently. We can then apply K-FAC to approximate the Fisher matrix below to perform updates simultaneously.

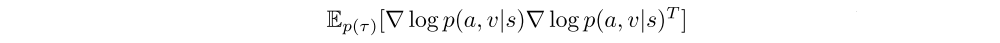
In addition, we use the `factorized Tikhonov damping（衰减）approach`. We also follow and perform the `asynchronous computation` of second-order statistics and inverses required by the Kronecker approximation to reduce computation time.

3.2 Step-size Selection and trust-region optimization

Traditionally, natural gradient is performed with SGD-like updates, θ ← θ − ηF−1∇θL. But in the context of deep RL, Schulman et al. observed that such an update rule can result in large updates to the policy, causing the algorithm to prematurely（过早地）converge to a near-deterministic policy. They advocate instead using a trust region approach, whereby the update is scaled down to modify the policy distribution (in terms of KL divergence) by at most a specified amount. Therefore, we `adopt the trust region formulation of K-FAC`, choosing the effective step size η to be

Slides

Abstract

We propose to apply trust region optimization to deep reinforcement learning using a recently proposed Kronecker-factored approximation to the curvature（曲率）.

We extend the framework of natural policy gradient and propose to optimize both the actor and the critic using Kronecker-factored approximate curvature (K-FAC) with trust region.

The first scalable trust region natural gradient method for actor-critic methods.

A method that learns non-trivial tasks in continuous control as well as discrete control policies directly from raw pixel inputs.

1 Introduction

Sample efficiency is a dominant concern in RL. One way to effectively reduce the sample size is to use more advanced optimization techniques for gradient updates.

In practice, the per-update computation cost of ACKTR is only 10% to 25% higher than SGD-based methods. Empirically, we show that ACKTR substantially improves both sample efficiency and the final performance of the agent.

2 Background

2.1 Reinforcement learning and actor-critic methods

2.2 Natural gradient using Kronecker-factored approximation

To minimize a nonconvex function J(θ), the method of steepest descent calculates the update ∆θ that minimizes J(θ + ∆θ), subject to the constraint that ||∆θ||B < 1, where || · ||B is the norm defined by

and B is a positive semidefinite matrix（半正定矩阵）. The solution to the constraint optimization problem has the form

K-FAC utilizes this fact and further approximates the block Fℓ (Fisher matrix) corresponding to layer ℓ as ˆFℓ,

This approximation can be interpreted as making the assumption that the second-order statistics of the activations and the backpropagated derivatives are uncorrelated. By exploiting the basic identities

And with the above approximation, the natural gradient update can be efficiently computed

From the above equation we see that the K-FAC approximate natural gradient update only requires computations on matrices comparable in size to W. The K-FAC algorithm has been extended to handle convolutional networks.

3 Methods

3.1 Natural gradient in actor-critic

To define the Fisher metric for reinforcement learning objectives, one natural choice is to use the policy function which defines a distribution over the action given the current state, and take the expectation over the trajectory distribution:

where p(τ) is the distribution of trajectories, given by

In practice, one approximates the intractable expectation over trajectories collected during training.

In addition, we use the factorized Tikhonov damping（衰减）approach. We also follow and perform the asynchronous computation of second-order statistics and inverses required by the Kronecker approximation to reduce computation time.

3.2 Step-size Selection and trust-region optimization

Sample efficiency is a dominant concern in RL. One way to effectively reduce the sample size is to use `more advanced optimization techniques for gradient updates`.

In practice, the per-update computation cost of ACKTR is `only 10% to 25% higher than SGD-based methods`. Empirically, we show that ACKTR substantially `improves both sample efficiency and the final performance` of the agent.

To minimize a nonconvex function J(θ), the `method of steepest descent` calculates the update ∆θ that minimizes J(θ + ∆θ), subject to the constraint that ||∆θ||B < 1, where || · ||B is the norm defined by

and `B is a positive semidefinite matrix（半正定矩阵）`. The solution to the constraint optimization problem has the form

K-FAC utilizes this fact and further `approximates the block Fℓ (Fisher matrix) corresponding to layer ℓ as ˆFℓ`,

This approximation can be interpreted as making the assumption that the second-order statistics of the activations and the backpropagated derivatives are `uncorrelated`. By exploiting the `basic identities`

And with the above approximation, the `natural gradient update` can be efficiently computed

From the above equation we see that the K-FAC approximate natural gradient update only requires `computations on matrices comparable in size to W`. The K-FAC algorithm has been `extended to handle convolutional networks`.

To `define the Fisher metric` for reinforcement learning objectives, one natural choice is to use the policy function which defines a distribution over the action given the current state, and take the expectation over the trajectory distribution:

where p(τ) is the `distribution of trajectories`, given by

In addition, we use the `factorized Tikhonov damping（衰减）approach`. We also follow and perform the `asynchronous computation` of second-order statistics and inverses required by the Kronecker approximation to reduce computation time.