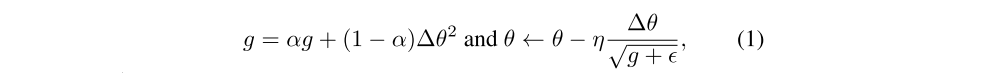Abstract

  • A conceptually simple and lightweight framework for DRL that uses asynchronous gradient descent for optimization of DNN controllers

  • Parallel actor-learners have a stabilizing effect on training allowing all four variants to successfully train neural network controllers

  • Asynchronous actor-critic succeeds on a wide variety of continuous motor control problems

1 Introduction

It was previously thought that the combination of simple online RL algorithms with deep neural networks was fundamentally unstable.

The solutions that have been proposed to stabilize the algorithm share a common idea: the sequence of observed data encountered（遇到） by an online RL agent is non-stationary, and online RL updates are strongly correlated.

The experience replay buffer can reduce non-stationarity and decorrelate updates. However, at the same time, it has several drawbacks. It requires off-policy learning algorithms that can update from data generated by an older policy. It uses more memory and computation per real interaction.

This paper provides a very different paradigm for DRL. Instead of experience replay, we asynchronously execute multiple agents in parallel, on multiple instances of the environment. This parallelism also decorrelates the agents’ data into a more stationary process, since at any given time-step the parallel agents will be experiencing a variety of different states. This simple idea

enables a much larger spectrum of fundamental on-policy RL algorithms.

Practical benefits: our experiments can run on a single machine

with a standard multi-core CPU instead of GPUs or massively distributed architectures; better results; far less time.

The best of the proposed methods is asynchronous advantage actor-critic (A3C), which is successful on both 2D and 3D games, discrete and continuous action spaces. - more general

3. Reinforcement Learning Background (Review)

In one-step Q-learning, the parameters θ of the action value function Q(s,a;θ) are learned by iteratively minimizing a sequence of loss functions, where the ith loss function defined as


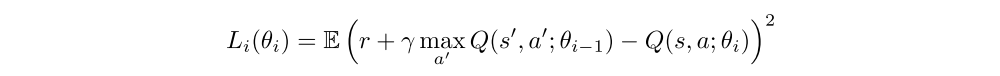
One drawback of using one-step methods is that obtaining a reward r only directly affects the value of the state action pair that leads to the reward. This can make the learning process slow since many updates are required the propagate a reward to the relevant

preceding states and actions.

One way of propagating rewards faster is by using n-step returns. This way results in a single reward r directly affecting the values of n preceding state action pairs. This makes the process of propagating rewards to relevant state-action pairs potentially much more efficient.

Policy-based model-free methods directly parameterize the policy π(a|s; θ) and update the parameters θ by performing, typically approximate, gradient ascent on E[Rt].

Standard REINFORCE updates the policy parameters θ in the direction


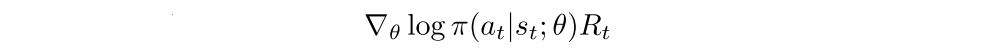
which is an unbiased estimate of ∇θE[Rt].

It is possible to reduce the variance of this estimate while keeping it unbiased by subtracting a learned function of the state bt(st), known as a baseline from the return. The result gradient is


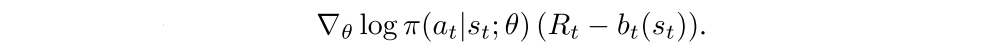
A learned estimate of the value function is commonly used as the baseline bt(st) ≈ Vπ(st) leading to a much lower variance estimate of the policy gradient. When an approximate value function is used as the baseline, the quantity Rt−bt used to scale the policy gradient can be seen as an estimate of the advantage of action at in state st


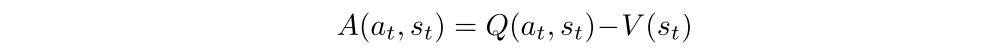
This approach can be viewed as an actor-critic architecture where the policy π is the actor and the baseline bt is the critic.

4 Asynchronous RL Framework

We design multi-threaded asynchronous variants to find RL algorithms that can train DNN policies reliably and without large resource requirements.

  1. We use asynchronous actor-learners, instead of using separate machines and a parameter server, we use multiple CPU threads on a single machine. Keeping the learners on a single machine removes the communication costs of sending gradients and parameters and enables us to use Hogwild! style updates for training, which is a asynchronous stochastic gradient descent algorithm.

  2. Make the observation that multiple actor-learners running in parallel are likely to be exploring different parts of the environment. One can explicitly use different exploration policies in each actor-learner to maximize this diversity. Then the overall changes being made to the parameters by multiple actor-learners applying online updates in parallel are likely to be less correlated in time than a single agent applying online updates. We don’t need replay memory to stabilize learning any more.

  3. Other practical benefits:

    • A reduction in training time that is roughly linear in the number of parallel actor-learners.

    • Be able to use on-policy RL methods such as Sarsa and actor-critic to train neural networks in a stable way.

We now describe the asynchronous advantage actor-critic (A3C): The algorithm maintains a policy π(at|st; θ) and an estimate of the value function V(st; θv). Our variant of actor-critic uses the same mix of n-step returns to update both the policy and the value function. The policy and the value function are updated after every tmax actions or when a terminal state is reached. The update performed by the algorithm can be seen as


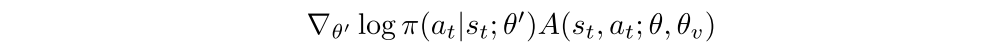
where A(st, at; θ, θv) is an estimate of the advantage function given by


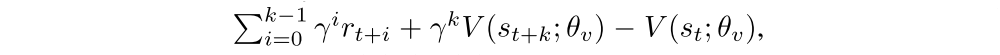
where k can vary from state to state and is upper-bounded by tmax. The following is the pseudocode for the algorithm.


As with the value-based methods we rely on parallel actor- learners and accumulated updates for improving training stability. Note that while the parameters θ of the policy and θv of the value function are shown as being separate for generality, we always share some of the parameters in practice. We typically use a CNN that has one softmax output for the policy π(at|st; θ) and one linear output for the value function V(st; θv), with all non-output layers shared.

We also found that adding the entropy of the policy π to the objective function improved exploration by discouraging premature convergence to suboptimal deterministic policies. It was particularly helpful on tasks requiring hierarchical behavior. The gradient of the full objective function including the entropy regularization term with respect to the policy parameters takes the form


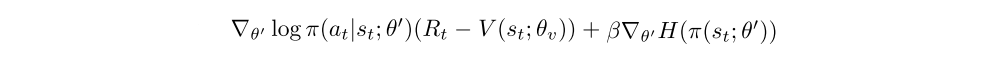
where H is the entropy. The hyperparameter β controls the strength of the entropy regularization term.

To do the optimization, we used the standard no-centered RMSProp (with shared statistics) update given by


where all operations are performed elementwise. A comparison on a subset of Atari 2600 games showed that a variant of RMSProp where statistics g are shared across threads is considerably more robust.