Paper 11: Deterministic Policy Gradient Algorithms (DPG)
Abstract
-
We consider deterministic policy gradient algorithms for reinforcement learning with continuous actions.
-
The deterministic policy gradient is the expected gradient of the action-value function, so it can be estimated much more efficiently than the usual stochastic policy gradient.
-
To ensure adequate exploration, we introduce an off-policy actor-critic algorithm that learns a deterministic target policy from an exploratory behaviour policy.
1 Introduction
We show that the deterministic policy gradient does indeed exist, and furthermore it has a simple model-free form that simply follows the gradient of the action-value function.
In the stochastic case, the policy gradient integrates over both state and action spaces, whereas in the deterministic case it only integrates over the state space. As a result, computing the stochastic policy gradient may require more samples, especially if the action space has many dimensions.
To ensure that our deterministic policy gradient algorithms continue to explore satisfactorily, we introduce an off-policy learning algorithm. The basic idea is to choose actions according to a stochastic behaviour policy (to ensure adequate exploration), but to learn about a deterministic target policy (exploiting the efficiency of the deterministic policy gradient).
We use the deterministic policy gradient to derive an off-policy actor-critic algorithm that estimates the action-value function using a differentiable function approximator, and then updates the policy parameters in the direction of the approximate action-value gradient.
We also introduce a notion of compatible(兼容的)function approximation for deterministic policy gradients, to ensure that the approximation does not bias the policy gradient.
Our algorithms require no more computation than prior methods: the computational cost of each update is linear in the action dimensionality and the number of policy parameters.
2 Background
-
Preliminaries
We denote the density at state s’ after transitioning for t time steps from state s by p(s → s’, t, π). We also denote the (improper) discounted state distribution by
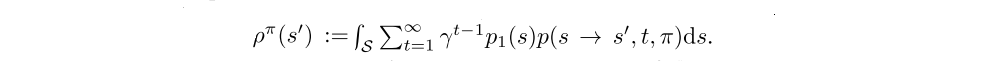
We can then write the performance objective as an expectation,
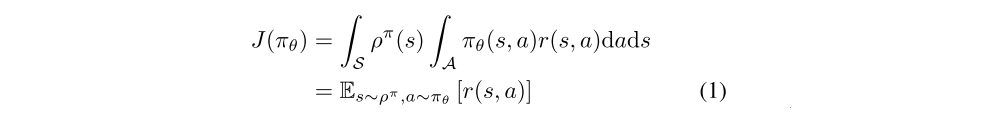
where Es∼ρ [·] denotes the (improper) expected value with respect to discounted state distribution ρ(s).
-
Stochastic Policy Gradient Theorem
The basic idea behind Policy gradient algorithms is to adjust the parameters θ of the policy in the direction of the performance gradient ∇θJ(πθ). The fundamental result underlying these algorithms is the policy gradient theorem,
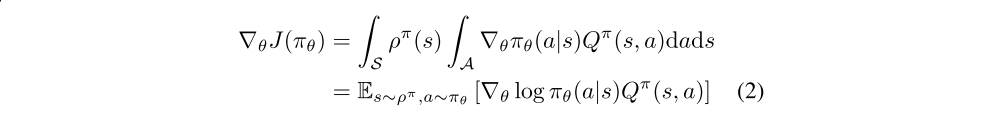
Despite the fact that the state distribution ρπ(s) depends on the policy parameters, the policy gradient does not depend on the gradient of the state distribution.
The policy gradient theorem has been used to derive a variety of policy gradient algorithms, by forming a sample-based estimate of this expectation. One issue that these algorithms must address is how to estimate the action-value function Qπ(s, a). Perhaps the simplest approach is to use a sample return to estimate the value of Qπ(st, at), which leads to a variant of the REINFORCE algorithm.
-
Stochastic Actor-Critic Algorithms
For the critic, in general, substituting a function approximator Qw(s, a) for the true action-value function Qπ(s, a) may introduce bias. However, if the function approximator is compatible such that i)
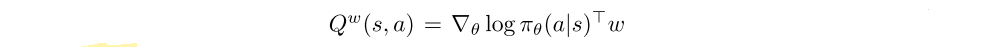
and ii) the parameters w are chosen to minimize the mean-squared error
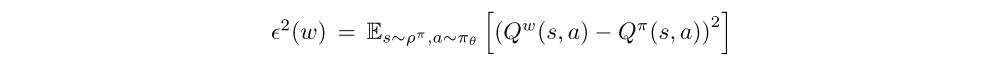
then there is no bias.
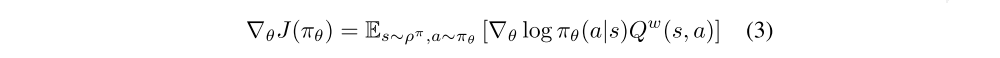
-
Off-Policy Actor-Critic
It is often useful to estimate the policy gradient off-policy from trajectories sampled from a distinct behaviour policy β(a|s) ≠ πθ(a|s). In an off-policy setting, the performance objective is typically modified to be the value function of the target policy, averaged over the state distribution of the behaviour policy,
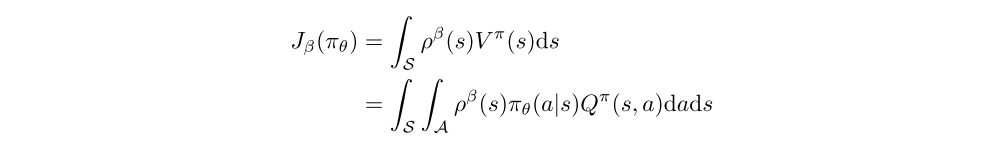
Differentiating the performance objective and applying an approximation gives the off-policy policy-gradient
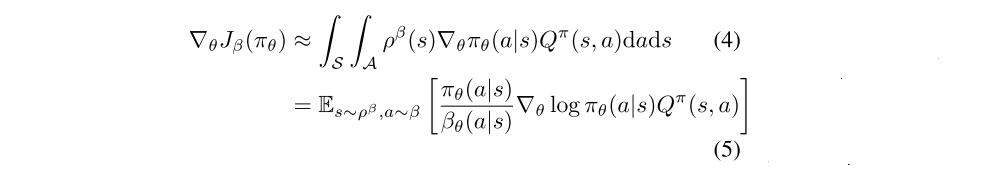
This approximation drops a term that depends on the action-value gradient ∇θQπ(s, a).
3 Gradients of Deterministic Policies
We now consider how the policy gradient framework may be extended to deterministic policies. Our main result is a deterministic policy gradient theorem. We provide several ways to derive and understand this result.
-
First we provide an informal intuition behind the form of the deterministic policy gradient.
-
We then give a formal proof of the deterministic policy gradient theorem from first principles.
-
Finally, we show that the deterministic policy gradient theorem is in fact a limiting case of the stochastic policy gradient theorem.
3.1 Action-Value Gradients
In continuous action spaces, we move the policy in the direction of the gradient of Q, rather than globally maximizing Q. Each state suggests a different direction of policy improvement; these may be averaged together by taking an expectation with respect to the state distribution ρµ(s),
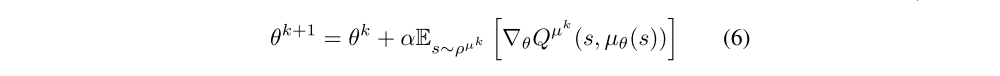
By applying the chain rule we see that the policy improvement may be decomposed into the gradient of the action-value with respect to actions, and the gradient of the policy with respect to the policy parameters.
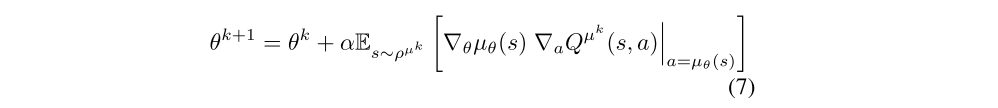
By convention ∇θµθ(s) is a Jacobian matrix such that each column is the gradient ∇θ[µθ(s)]d of the dth action dimension of the policy with respect to the policy parameters θ. However, by changing the policy, different states are visited and the state distribution ρµ will change. As a result it is not immediately obvious that this approach guarantees improvement, without taking account of the change to distribution. However, the theory below shows that, like the stochastic policy gradient theorem, there is no need to compute the gradient of the state distribution; and that the intuitive update outlined above is following precisely the gradient of the performance objective.
3.2 Deterministic Policy Gradient Theorem
We write the performance objective as an expectation again,
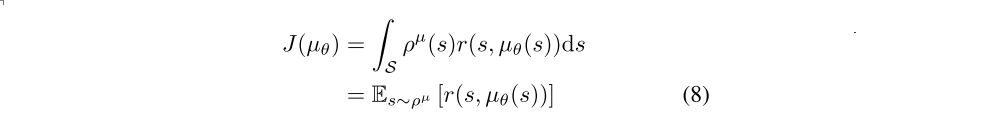
We now provide the deterministic policy gradient theorem analogue to the policy gradient theorem.

3.3 Limit of the Stochastic Policy Gradient
The deterministic policy gradient is indeed a special (limiting) case of the stochastic policy gradient - variance parameter σ = 0.

4 Deterministic Actor-Critic Algorithms
We now use the deterministic policy gradient theorem to derive both on-policy and off-policy actor-critic algorithms.
4.1 On-Policy Deterministic Actor-Critic
In general, behaving according to a deterministic policy will not ensure adequate exploration and may lead to sub-optimal solutions.
Like the stochastic actor-critic, the deterministic actor-critic consists of two components.
In the following deterministic actor-critic algorithm, the critic uses Sarsa updates to estimate the action-value function.
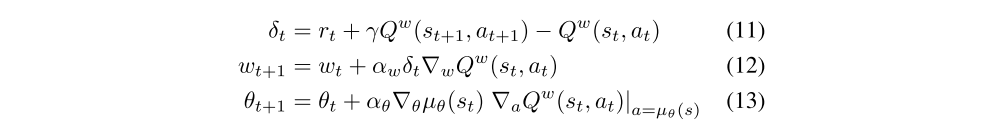
4.2 Off-Policy Deterministic Actor-Critic
We now consider off-policy methods that learn a deterministic target policy µθ(s) from trajectories generated by an arbitrary stochastic behaviour policy π(s, a). As before, we modify the performance objective to be the value function of the target policy, averaged over the state distribution of the behaviour policy,
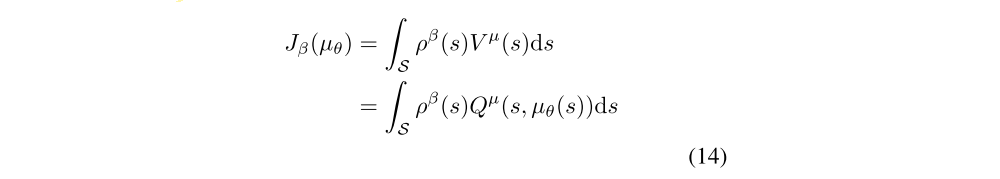
The off-policy deterministic policy gradient
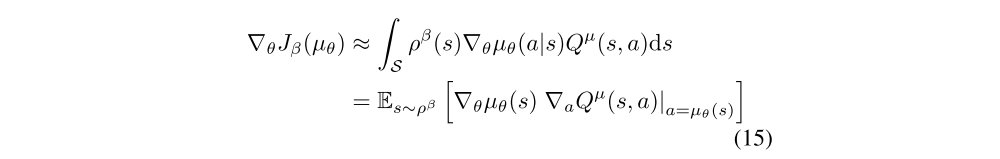
We now develop an actor-critic algorithm that updates the policy in the direction of the off-policy deterministic policy gradient. In the following off-policy deterministic actor-critic (OPDAC) algorithm, the critic uses Q-learning updates to estimate the action-value function.
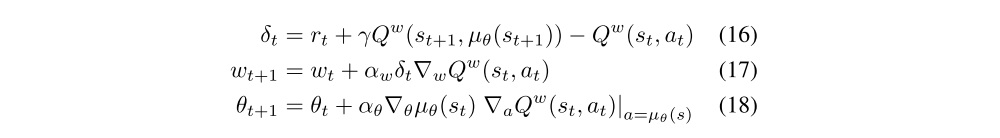
Because the deterministic policy gradient removes the integral over actions, we can avoid importance sampling in the actor; and by using Q-learning, we can avoid importance sampling in the critic.
4.3 Compatible Function Approximation
In general, substituting an approximate Qw(s, a) into the deterministic policy gradient will not necessarily follow the true gradient (nor indeed will it necessarily be an ascent direction at all). We find a critic Qw(s, a) such that the gradient ∇aQµ(s, a) can be replaced by ∇aQw(s, a), without affecting the deterministic policy gradient.
