Abstract

  • We present an actor-critic, model-free algorithm based on the deterministic policy gradient that can operate over continuous action spaces.

  • Our algorithm is able to find policies whose performance is competitive with those found by a planning algorithm with full access to the dynamics of the domain and its derivatives.

  • We further demonstrate that for many of the tasks the algorithm can learn policies “end-to-end”: directly from raw pixel inputs.

1 Introduction

In this work we present a model-free, off-policy actor-critic algorithm using deep function approximators that can learn policies in high-dimensional, continuous action spaces.

Our work is based on the deterministic policy gradient (DPG) algorithm. However, as we show below, a naive application of this actor-critic method with neural function approximators is unstable for challenging problems. Here we combine the actor-critic approach with insights from the recent success of Deep Q Network (DQN).

DQN is able to learn value functions using function approximators in a stable and robust way due to two innovations:

  1. The network is trained off-policy with samples from a replay buffer to minimize correlations between samples;

  2. The network is trained with a target Q network to give consistent targets during temporal difference backups. In this work we make use of the same ideas, along with batch normalization, a recent advance in deep learning.

A key feature of the approach is its simplicity: it requires only a straightforward actor-critic architecture and learning algorithm with very few “moving parts”, making it easy to implement and scale to more difficult problems and larger networks.

2 Background

Action-value function describes the expected return after taking an action at in state st and thereafter following policy π:


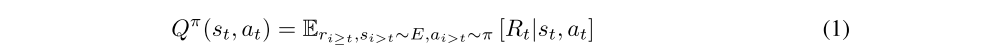
Many approaches in reinforcement learning make use of the recursive relationship known as the Bellman equation:


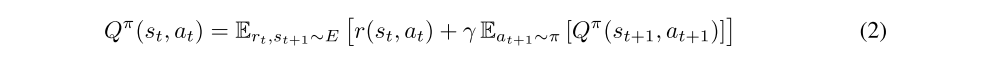
If the target policy is deterministic we can describe it as a function µ : S ← A and avoid the inner expectation:


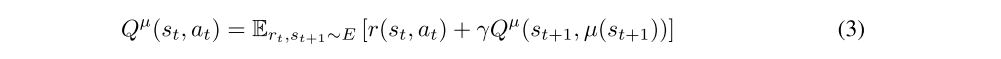
The expectation depends only on the environment. This means that it is possible to learn Qµ off-policy, using transitions which are generated from a different stochastic behavior policy β.

For Q-learning, we consider function approximators parameterized by θQ, which we optimize by minimizing the loss:


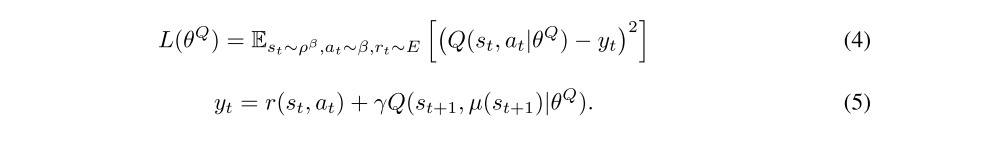
Recently, the Q-learning has been adapted to make effective use of large neural networks as function approximators. In order to scale Q-learning we introduced two major changes: the use of a replay buffer, and a separate target network for calculating yt. We employ these in the context of DDPG and explain their implementation in the next section.

3 Algorithm

Here we used an actor-critic approach based on the DPG algorithm. The DPG algorithm maintains a parameterized actor function µ(s|θµ) which specifies the current policy by deterministically mapping states to a specific action. The critic Q(s, a) is learned using the Bellman equation as in Q-learning. The actor is updated by following the applying the chain rule to the expected return from the start distribution J with respect to the actor parameters:


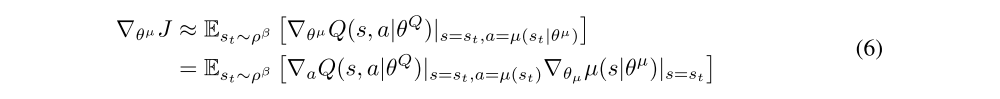
Our contribution here is to provide modifications to DPG, inspired by the success of DQN, which allow it to use neural network function approximators to learn in large state and action spaces online. We refer to our algorithm as Deep DPG (DDPG).


  • Challenge 1

when using neural networks for reinforcement learning is that most optimization algorithms assume that the samples are independently and identically distributed (iid). Obviously, when the samples are generated from exploring sequentially in an environment this assumption no longer holds. Additionally, to make efficient use of hardware optimizations, it is essential to learn in mini-batches, rather than online.

As in DQN, we used a replay buffer to address these issues. The replay buffer is a finite sized cache R. Transitions were sampled from the environment according to the exploration policy and the tuple (st, at, rt, st+1) was stored in the replay buffer. When the replay buffer was full the oldest samples were discarded. At each timestep the actor and critic are updated by sampling a minibatch uniformly from the buffer. Because DDPG is an off-policy algorithm, the replay buffer can be large, allowing the algorithm to benefit from learning across a set of uncorrelated transitions.

  • Challenge 2

Directly implementing Q learning with neural networks proved to be unstable in many environments. Since the network Q(s, a|θQ) being updated is also used in calculating the target value, the Q update is prone to divergence.

Our solution is similar to the target network but modified for actor-critic and using “soft” target updates, rather than directly copying the weights. We create a copy of the actor and critic networks, Q’(s, a|θQ’) and µ’(s|θµ’) respectively, that are used for calculating the target values. The weights of these target networks are then updated by having them slowly track the learned networks: θ' ← τθ + (1 − τ)θ' with τ « 1. This means that the target values are constrained to change slowly, greatly improving the stability of learning. This simple change moves the relatively unstable problem of learning the action-value function closer to the case of supervised learning, a problem for which robust solutions exist. We found that having both a target µ’ and Q’ was required to have stable targets yi in order to consistently train the critic without divergence. This may slow learning, since the target network delays the propagation of value estimations. However, in practice we found this was greatly outweighed by the stability of learning.

  • Challenge 3

When learning from low dimensional feature vector observations, the different components of the observation may have different physical units (for example, positions versus velocities) and the ranges may vary across environments. This can make it difficult for the network to learn effectively and may make it difficult to find hyper-parameters which generalize across environments with different scales of state values.

One approach to this problem is to manually scale the features so they are in similar ranges across environments and units. We address this issue by adapting a recent technique from deep learning called batch normalization. This technique normalizes each dimension across the samples in a minibatch to have unit mean and variance. In addition, it maintains a running average of the mean and variance to use for normalization during testing (in our case, during exploration or evaluation). In deep networks, it is used to minimize covariance shift during training, by ensuring that each layer receives whitened input. In the low-dimensional case, we used batch normalization on the state input and all layers of the µ network and all layers of the Q network prior to the action input. With batch normalization, we were able to learn effectively across many different tasks with differing types of units, without needing to manually ensure the units were within a set range.

  • Challenge 4

A major challenge of learning in continuous action spaces is exploration.

An advantage of off-policies algorithms such as DDPG is that we can treat the problem of exploration independently from the learning algorithm. We constructed an exploration policy µ’ by adding noise sampled from a noise process N to our actor policy


N can be chosen to suit the environment. We used an Ornstein-Uhlenbeck process to generate temporally correlated exploration for exploration efficiency in physical control problems with inertia.