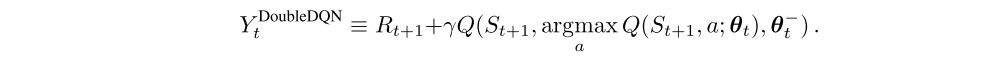Paper 13: Deep Reinforcement Learning with Double Q-learning (Double DQN)
Abstract
-
We answer the questions whether overestimations are common, whether they harm performance, and whether they can generally be prevented.
-
We show that the idea behind the Double Q-learning algorithm, which was introduced in a tabular setting, can be generalized to work with large-scale function approximation.
-
We propose a specific adaptation to the DQN algorithm and show that the resulting algorithm not only reduces the observed overestimations, as hypothesized, but that this also leads to much better performance on several games.
1 Background
Most interesting problems are too large to learn all action values in all states separately. Instead, we can learn a parameterized value function Q(s, a; θt). The standard Q-learning update for the parameters after taking action At in state St and observing the immediate reward Rt+1 and resulting state St+1 is then
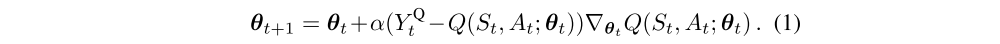
where α is a scalar step size and the target is defined as
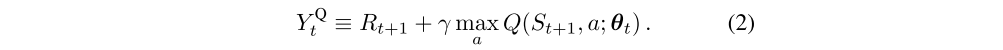
-
Deep Q Networks
Two important ingredients of the DQN algorithm are the use of a target network, and the use of experience replay. The target network, with parameters θ−, is the same as the online network except that its parameters are copied every τ steps from the online network, so that then θ−t = θt, and kept fixed on all other steps. The target used by DQN is then
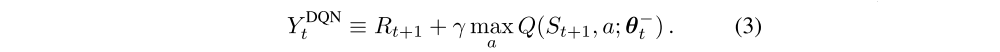
-
Double Q-learning
In the original Double Q-learning algorithm, two value functions are learned by assigning each experience randomly to update one of the two value functions, such that there are two sets of weights, θ and θ’. For each update, one set of weights is used to determine the greedy policy and the other to determine its value. For a clear comparison, we can first untangle the selection and evaluation in Q-learning and rewrite its target (2) as
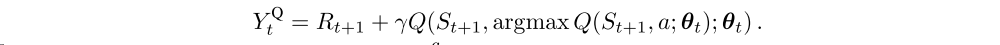
The Double Q-learning error can then be written as
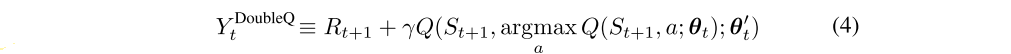
2 Overoptimism due to estimation errors
In this section we demonstrate more generally that estimation errors of any kind can induce an upward bias, regardless of whether these errors are due to environmental noise, function approximation, non-stationarity, or any other source. This is important, because in practice any method will incur some inaccuracies during learning, simply due to the fact that the true values are initially unknown.
3 Double DQN
The idea of Double Q-learning is to reduce overestimations by decomposing the max operation in the target into action selection and action evaluation. Although not fully decoupled, the target network in the DQN architecture provides a natural candidate for the second value function, without having to introduce additional networks. We therefore propose to evaluate the greedy policy according to the online network, but using the target network to estimate its value. In reference to both Double Q-learning and DQN, we refer to the resulting algorithm as Double DQN. Its update is the same as for DQN, but replacing the target with