Paper 14: Addressing Function Approximation Error in Actor-Critic Methods (TD3)
Abstract
-
In value-based reinforcement learning methods such as deep Q-learning, function approximation errors are known to lead to overestimated value estimates and suboptimal policies.
-
We show that this problem persists in an actor-critic setting and propose novel mechanisms to minimize its effects on both the actor and the critic.
-
Our algorithm builds on Double Q-learning, by taking the mini-mum value between a pair of critics to limit overestimation.
-
We draw the connection between target networks and overestimation bias, and suggest delaying policy updates to reduce per-update error and further improve performance.
1 Introduction
The issue of value overestimation (as a result of function approximation errors) with actor-critic methods in continuous control domains have been largely left untouched. In this paper, we show overestimation bias and the accumulation of error in temporal difference methods are present in an actor-critic setting. Our proposed method addresses these issues, and greatly outperforms the current state of the art.
In this paper,
-
we begin by establishing this overestimation property is also present for deterministic policy gradients, in the continuous control setting.
-
then we adapt an older variant, Double Q-learning, to an actor-critic format by using a pair of independently trained critics.
-
but to address the concern of high variance, we propose a clipped Double Q-learning variant which leverages the notion that a value estimate suffering from overestimation bias can be used as an approximate upper-bound to the true value estimate.
Given the connection of noise to overestimation bias, this paper contains a number of components that address variance reduction.
-
First, we show that target networks, a common approach in deep Q-learning methods, are critical for variance reduction by reducing the accumulation of errors.
-
Second, to address the coupling of value and policy, we propose delaying policy updates until the value estimate has converged.
-
Finally, we introduce a novel regularization strategy, where a SARSA-style update bootstraps similar action estimates to further reduce variance.
Our modifications are applied to DDPG form the Twin Delayed Deep Deterministic policy gradient algorithm (TD3), an actor-critic algorithm which considers the interplay(相互影响)between function approximation error in both policy and value updates.
3 Background
In actor-critic methods, the policy, known as the actor, can be updated through the deterministic policy gradient algorithm
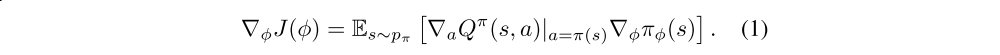
The Bellman equation is a fundamental relationship between the value of a state-action pair (s, a) and the value of the subsequent state-action pair (s’, a’):
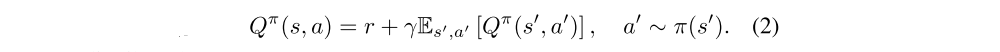
In deep Q-learning, the network is updated by using temporal difference learning with a secondary frozen target network Qθ’(s, a) to maintain a fixed objective y over multiple updates:
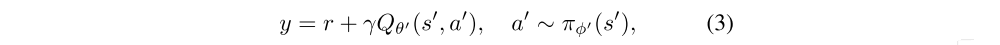
4 Overestimation Bias
In Q-learning with discrete actions, the value estimate is updated with a greedy target. however, if the target is susceptible to error ε, then the maximum over the value along with its error will generally be greater than the true maximum
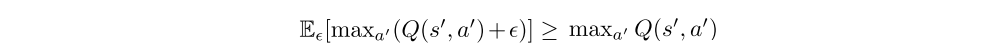
As a result, even initially zero-mean error can cause value updates to result in a consistent overestimation bias, which is then propagated through the Bellman equation. This is problematic as errors induced by function approximation are unavoidable.
While in the discrete action setting overestimation bias is an obvious artifact from the analytical maximization, the presence and effects of overestimation bias is less clear in an actor-critic setting where the policy is updated via gradient descent. We begin by proving that the value estimate in deterministic policy gradients will be an overestimation under some basic assumptions and then propose a clipped variant of Double Q-learning in an actor-critic setting to reduce overestimation bias.
4.1 Overestimation Bias in Actor-Critic
In actor-critic methods the policy is updated with respect to the value estimates of an approximate critic. In this section we assume the policy is updated using the deterministic policy gradient, and show that the update induces overestimation in the value estimate. Given current policy parameters φ, let φapprox define the parameters from the actor update induced by the maximization of the approximate critic Qθ(s, a) and φtrue the parameters from the hypothetical(假想的)actor update with respect to the true underlying value function Qπ(s, a) (which is not known during learning):
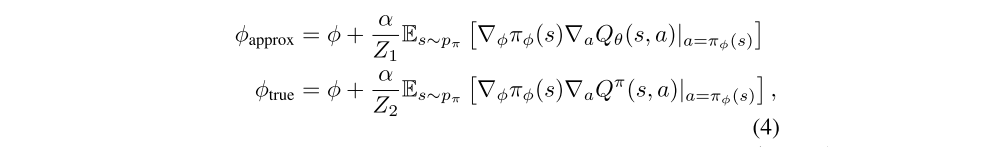
where we assume Z1 and Z2 are chosen to normalize the gradient, i.e., such that Z−1||E[·]|| = 1. Without normalized gradients, overestimation bias is still guaranteed to occur with slightly stricter conditions. We denote πapprox and πtrue as the policy with parameters φapprox and φtrue respectively.
As the gradient direction is a local maximizer, there exists ε1 value of πapprox will be bounded below by the approximate sufficiently small such that if α ≤ ε1 then the approximate value of πtrue:
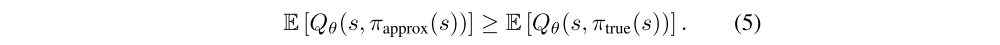
Conversely, there exists ε2 sufficiently small such that if α ≤ ε2 then the true value of πapprox will be bounded above by the true value of πtrue:
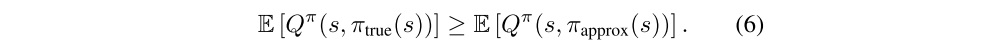
If in expectation the value estimate is at least as large as the true value with respect to φtrue, E[Qθ(s, πtrue(s))] ≥ E[Qπ(s, πtrue(s))], then Equations (5) and (6) imply that if α < min(ε1, ε2), then the value estimate will be overestimated:
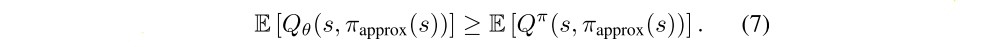
Although this overestimation may be minimal with each update, the presence of error raises two concerns.
-
Firstly, the overestimation may develop into a more significant bias over many updates if left unchecked.
-
Secondly, an inaccurate value estimate may lead to poor policy updates. This is particularly problematic because a feedback loop is created, in which suboptimal actions might be highly rated by the suboptimal critic, reinforcing the suboptimal action in the next policy update.
This theoretical overestimation occur in practice for state-of-the-art methods.
4.2. Clipped Double Q-Learning for Actor-Critic
This section introduces a novel clipped variant of Double Q-learning, which can replace the critic in any actor-critic method.
In Double DQN, the authors propose using the target network as one of the value estimates, and obtain a policy by greedy maximization of the current value network rather than the target network. In an actor-critic setting, an analogous update uses the current policy rather than the target policy in the learning target:
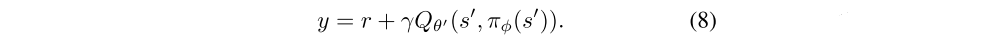
In practice however, we found that with the slow-changing policy in actor-critic, the current and target networks were too similar to make an independent estimation, and offered little improvement. Instead, the original Double Q-learning formulation can be used, with a pair of actors (πφ1, πφ2) and critics (Qθ1, Qθ2), where πφ1 is optimized with respect to Qθ1 and πφ2 with respect to Qθ2:
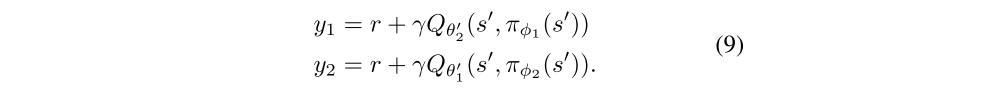
As πφ1 optimizes with respect to Qθ1, using an independent estimate in the target update of Qθ1 would avoid the bias introduced by the policy update. However the critics are not entirely independent, due to the use of the opposite critic in the learning targets, as well as the same replay buffer. As a result, for some states s we will have Qθ2(s, πφ1(s)) > Qθ1(s, πφ1(s)). This is problematic because Qθ1(s, πφ1 (s)) will generally overestimate the true value, and in certain areas of the state space the overestimation will be further exaggerated(夸大). To address this problem, we propose to simply upper-bound the less biased value estimate Qθ2 by the biased estimate Qθ1. This results in taking the minimum between the two estimates, to give the target update of our Clipped Double Q-learning algorithm:
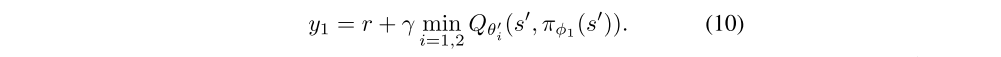
In implementation, computational costs can be reduced by using a single actor optimized with respect to Qθ1. We then use the same target y2 = y1 for Qθ2.
5 Addressing Variance
In this section we emphasize the importance of minimizing error at each update, build the connection between target networks and estimation error and propose modifications to the learning procedure of actor-critic for variance reduction.
5.1 Accumulating Error
Each update leaves some amount of residual TD-error δ(s, a):
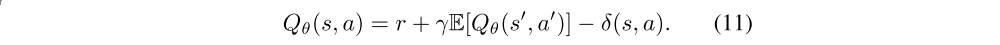
Rather than learning an estimate of the expected return, the value estimate approximates the expected return minus the expected discounted sum of future TD-errors:
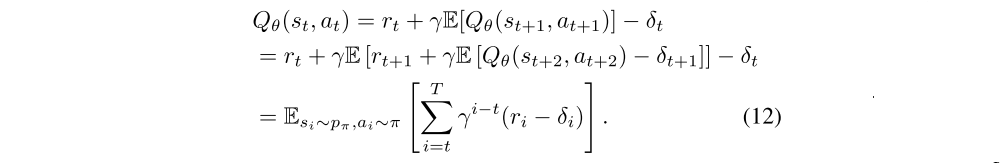
If the value estimate is a function of future reward and estimation error, it follows that the variance of the estimate will be proportional to the variance of future reward and estimation error. Given a large discount factor γ, the variance can grow rapidly with each update if the error from each update is not tamed.
5.2 Target Networks and Delayed Policy Updates
In this section we examine the relationship between target networks and function approximation error, and show the use of a stable target reduces the growth of error. This insight allows us to consider the interplay between high variance estimates and policy performance, when designing reinforcement learning algorithms.
Results suggest that the divergence that occurs without target networks is the result of policy updates with a high variance value estimate.
If target networks can be used to reduce the error over multiple updates, and policy updates on high-error states cause divergent behavior, then the policy network should be updated at a lower frequency than the value network, to first minimize error before introducing a policy update. We propose delaying policy updates until the value error is as small as possible. The modification is to only update the policy and target networks after a fixed number of updates d to the critic. To ensure the TD-error remains small, we update the target networks slowly θ’ ← τθ + (1 − τ)θ’.
5.3 Target Policy Smoothing Regularization
We introduce a regularization strategy for deep value learning, target policy smoothing, which mimics the learning update from SARSA. Our approach enforces the notion that similar actions should have similar value. While the function approximation does this implicitly, the relationship between similar actions can be forced explicitly by modifying the training procedure. We propose that ` fitting the value of a small area around the target action`
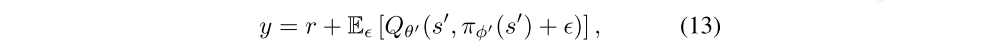
would have the benefit of smoothing the value estimate by bootstrapping off of similar state-action value estimates. In practice, we can approximate this expectation over actions by adding a small amount of random noise to the target policy and averaging over mini-batches. This makes our modified target update:
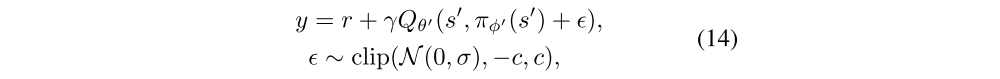
where the added noise is clipped to keep the target close to the original action.
