Introduction

If you have worked with neural networks, it is likely you have come across, or used, an Embedding layer to produce embeddings of categorical variables. When I first used an Embedding layer I only knew that it was some sort of layer that learned the best representations of a categorical input through the usual weight update of neural networks achieved by backpropagation. At that time I wondered, isn’t it exactly the same thing that a Dense (or Fully-Connected) layer does? Both kinds of layers, in fact, given an input, can produce a dense representation of it, that we can call an ‘embedding’. So what’s the difference between neural network Embedding and Dense layer?

The difference in a nutshell

The two main advantages of Embedding over Dense layers are reduced input size and reduced computational complexity, which results in speeding up the training time.

  1. Reduced input size

    Because Embedding layers are most commonly used in text processing, let’s take a sentence as a concrete example:

    ‘I am who I am’.

    Let’s first of all integer-encode the input:


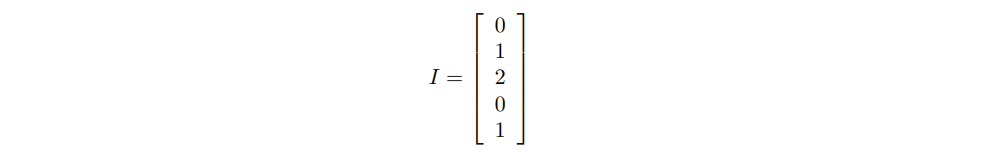
    A Dense layer requires the input to be strictly numerical. Thus, we need to one-hot encode it:


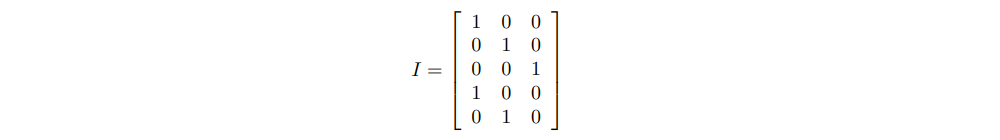
    Notice that the 1st dimension of this matrix represents the sentence length, while the 2nd dimension represents the number of unique words in our Corpus. Instead, the Embedding layer accepts the first input, the integer-encoded vector, which is much smaller. For this example, we imagined that the Corpus is made of only the 3 words that appear in our sentence: ‘I’, ‘am’, ‘who’. However, in real-life scenarios, the Corpus will be the whole English dictionary, made of about 180,000 words! Imagine having to keep in memory a 180,000 long vector for each single instance in our dataset, of which 99% will be made of zeros that do not contribute to the final output!

  2. Reduced computational complexity

    In order to obtain the input to hidden Dense layer, the network needs to perform matrix multiplication between the sparse one-hot-encoded matrix of the Input layer and a weight matrix. The Embedding layer, instead, considers the weight matrix as a mere lookup table, where the nth row represents the embedding vector of the nth integer-encoded level of the categorical input variable. In other words, a Dense layer performs a dot product operation, which is more computationally expensive than the select operation performed by the Embedding layer. This makes the training process much faster.

    However, the Embedding layer lacks of some trainable parameters, that are the bias and the activation function.

The difference with the Maths

Our one-hot encoded input is a 5 x 3 matrix. Let’s say we decide to use a 3-unit Dense Hidden Layer. Thus, our weight matrix W will be a 3 x 3 matrix. We initialize the weights at random as:


As stated above, the Dense layer performs a matrix multiplication to obtain its input.


The actual operation that happened is the following:


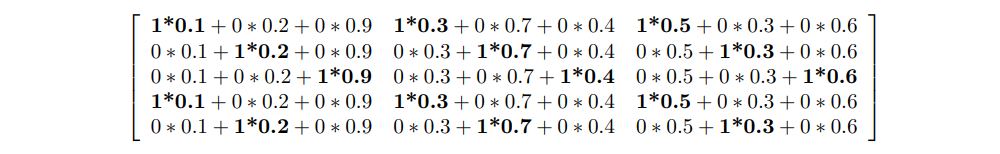
We had to perform a lot of multiplications by zero, and the resulting output is influenced only by the 1s. Is there any simpler and faster way? This is where the Embedding layer comes into play.

As stated above, there is no need to one-hot encode the Input when using an Embedding layer. While a Dense layer considers W as an actual weight matrix, an Embedding layer considers W as a simple lookup table. Moreover, it considers each integer in the Input array as the index where to find the relative weights in the lookup table. For the nth integer in the input I, the resulting vector is the nth row of the weight matrix:


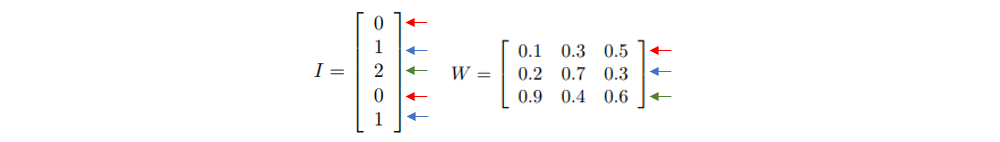
From which we can easily obtain the same output as obtained with the Dense layer:


Notice the meaning of this matrix. Each row is the ‘embedding’ representation of each word in our original sentence. Of course, because the first word ‘I’ was the same as the 4th word, the embedding representation is the same.

Combining Embedding and Dense Layers

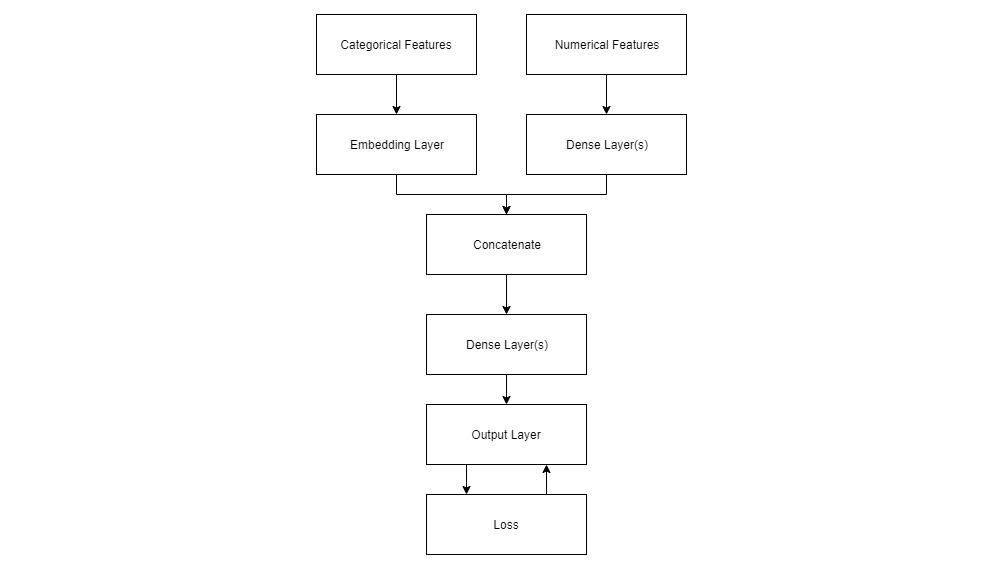
Can you use an Embedding layer to encode numerical features? No, it does not make sense. If the advantage of Embedding layers is that of skipping the one-hot encoding step, it is clear that we do not need an Embedding layer when one-hot encoding is not required in the first place! Thus, if your dataset includes both a set of highly-dimensional categorical variables and one of numerical variables, you should use an Embedding layer to encode the former and a Dense layer for the latter. These can then be concatenated and passed through the next layer. Moreover, we may use the embedding vector resulting from our Embedding layer, as input to a Dense layer. Our Network may thus look something like this:


torch.nn.Embedding


Conclusion

Embedding layers are a powerful tool to create dense and meaningful representations of high-dimensional categorical data. Their advantage over Dense layers lies in the smaller input size required and in the reduced computational complexity, which speeds up the training process.

Embedding layers have been widely used especially in word embeddings. The most popular example is perhaps Word2vec, which is only a 2-layer network that exploits an Embedding layer to transform words into a numeric format that can be used as input for a new network. Thus, although most online tutorials and papers mention Embedding layers in relation to text processing, this is not the only field in which they can be used. Virtually any categorical variable can be encoded using this powerful technique.