本文与上一篇论文 Noisy Networks for Exploration 一样，都是在网络的参数空间添加高斯噪声，但是上一篇论文的高斯噪声参数是通过基于强化学习损失函数的梯度下降学习出来的，而本文则是通过启发式的方法进行调节， 虽然没能实现端到端的学习，却也减少了参数的数量以及计算开销。

Abstract

  • DRL methods generally engage in exploratory behavior through noise injection in the action space. An alternative is to add noise directly to the agent’s parameters, which can lead to more consistent exploration and a richer set of behaviors. Methods such as evolutionary strategies use parameter perturbations, but discard all temporal structure in the process and require significantly more samples.

  • Combining parameter noise with traditional RL methods allows to combine the best of both worlds.

  • We demonstrate that both off- and on-policy methods benefit from this approach through experimental comparison of DQN, DDPG, and TRPO on high-dimensional discrete action environments as well as continuous control tasks.

1 Introduction

Exploration remains a key challenge in contemporary DRL. Its main purpose is to ensure that the agent’s behavior does not converge prematurely to a local optimum. Enabling efficient and effective exploration is, however, not trivial since it is not directed by the reward function of the underlying MDP. Although a plethora of methods have been proposed to tackle this challenge in high-dimensional and/or continuous-action MDPs, they often rely on complex additional structures such as counting tables, density modeling of the state space, learned dynamics models, or self-supervised curiosity.

This paper investigates how parameter space noise can be effectively combined with off-the-shelf DRL algorithms such as DQN2015, DDPG, and TRPO to improve their exploratory behavior. Experiments show that this form of exploration is applicable to both high-dimensional discrete environments and continuous control tasks, using on- and off-policy methods. Our results indicate that parameter noise outperforms traditional action space noise-based baselines, especially in tasks where the reward signal is extremely sparse.

2 Background

2.1 Off-policy Methods

  • Deep Q-Networks (DQN)

  • Deep Deterministic Policy Gradients (DDPG)

2.2 On-policy Methods

  • Trust Region Policy Optimization (TRPO)

3 Parameter Space Noise for Exploration

This work considers policies that are realized as parameterized functions, which we denote as πθ, with θ being the parameter vector. We represent policies as neural networks but our technique can be applied to arbitrary parametric models. To achieve structured exploration, we sample from a set of policies by applying additive Gaussian noise to the parameter vector of the current policy:


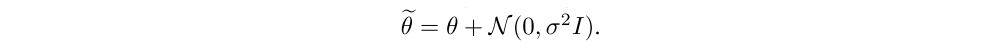
Importantly, the perturbed policy is sampled at the beginning of each episode and kept fixed for the entire rollout. For convenience and readability, we denote this perturbed policy π~:= πθ~ and analogously define π := πθ.

  • State-dependent exploration

There is a crucial difference between action space noise and parameter space noise. Consider the continuous action space case. When using Gaussian action noise, actions are sampled according to some stochastic policy,


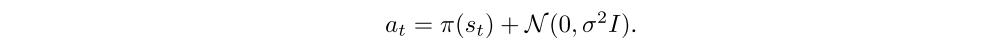
Therefore, even for a fixed state s, we will almost certainly obtain a different action whenever that state is sampled again in the rollout, since action space noise is completely independent of the current state st (notice that this is equally true for correlated action space noise). In contrast, if the parameters of the policy are perturbed at the beginning of each episode, we get at = π~(st) . In this case, the same action will be taken every time the same state st is sampled in the rollout. This ensures consistency in actions, and directly introduces a dependence between the state and the exploratory action taken.

  • Perturbing deep neural networks

It is not immediately obvious that DNNs, with potentially millions of parameters and complicated nonlinear interactions, can be perturbed in meaningful ways by applying spherical（球形的）Gaussian noise. However, as recently shown in some paper, a simple reparameterization of the network achieves exactly this. More concretely, we use layer normalization between perturbed layers. Due to this normalizing across activations within a layer, the same perturbation scale can be used across all layers, even though different layers may exhibit different sensitivities to noise.

深度神经网络中对权重添加参数噪声后，会引起前后层激活值分布发生变化。本文希望在每一层添加相同的噪声，但每层之间的噪声互不影响。因此，在深度神经网络中需要在每层添加 Layer Normalization，以增加训练的稳定性。

Batch Normalization 取不同样本的同一特征做归一化，而 Layer Normalization 取同一样本的不同通道做归一化。 Pytorch API

  • Adaptive noise scaling（噪声方差的自适应调节）

Parameter space noise requires us to pick a suitable scale σ. This can be problematic since

  1. the scale will strongly depend on the specific network architecture,

  2. and is likely to vary over time as parameters become more sensitive to noise as learning progresses.

  3. Additionally, while it is easy to intuitively grasp the scale of action space noise, it is far harder to understand the scale in parameter space.

We propose a simple solution that resolves all aforementioned limitations in an easy and straightforward way. This is achieved by adapting the scale of the parameter space noise over time and relating it to the variance in action space that it induces. More concretely, we can define a distance measure between perturbed and non-perturbed policy in action space and adaptively increase or decrease the parameter space noise depending on whether it is below or above a certain threshold:


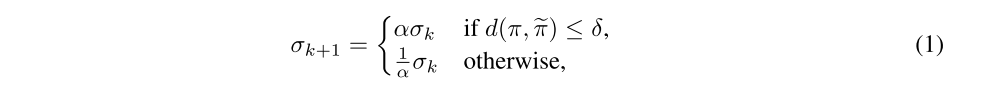
where α is a scaling factor and δ a threshold value. The concrete realization of d(·, ·) depends on the algorithm at hand and we describe appropriate distance measures for DQN, DDPG, and TRPO in Appendix C.

  • Parameter space noise for off-policy methods

In the off-policy case, parameter space noise can be applied straightforwardly since, by definition, data that was collected off-policy can be used. More concretely, we only perturb the policy for exploration and train the non-perturbed network on this data by replaying it.

  • Parameter space noise for on-policy methods

Parameter noise can be incorporated in an on-policy setting, using an adapted policy gradient, as set forth by previous paper in 2008. Policy gradient methods optimize


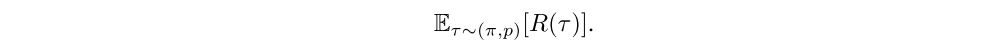
Given a stochastic policy πθ(a|s) with θ ∼ N(φ, Σ), the expected return can be expanded using likelihood ratios and the re-parametrization trick as