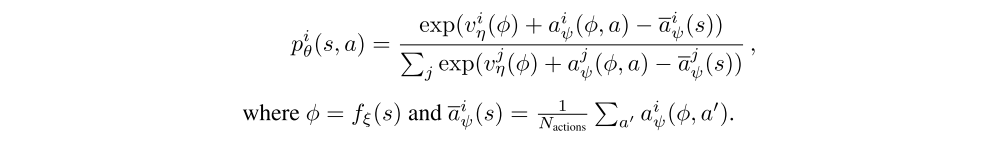Paper 47: Rainbow: Combining Improvements in Deep Reinforcement Learning
Abstract
-
The DRL community has made several independent improvements to the DQN algorithm. However, it is unclear which of these extensions are complementary and can be fruitfully combined.
-
This paper examines six extensions to the DQN algorithm and empirically studies their combination.
-
Our experiments show that the combination provides SOTA performance on the Atari 2600 benchmark, both in terms of data efficiency and final performance.
-
We also provide results from a detailed ablation study that shows the contribution of each component to overall performance.
1 Introduction
-
Double DQN addresses an overestimation bias of Q-learning, by decoupling selection and evaluation of the bootstrap action.
-
Prioritized experience replay improves data efficiency, by replaying more often transitions from which there is more to learn.
-
The dueling network architecture helps to generalize across actions by separately representing state values and action advantages.
-
Learning from multi-step bootstrap targets, as used in A3C, shifts the bias-variance trade-off and helps to propagate newly observed rewards faster to earlier visited states.
-
Distributional Q-learning learns a categorical distribution of discounted returns, instead of estimating the mean.
-
Noisy DQN uses stochastic network layers for exploration.
Each of these algorithms enables substantial performance improvements in isolation. Since they do so by addressing radically different issues, and since they build on a shared framework, they could plausibly be combined. In this paper we propose to study an agent that combines all the aforementioned ingredients. We show how these different ideas can be integrated, and that they are indeed largely complementary.
3 Extensions to DQN
-
Double Q-learning.
Conventional Q-learning is affected by an overestimation bias, due to the maximization step, and this can harm learning. Double Q-learning, addresses this overestimation by decoupling, in the maximization performed for the bootstrap target, the selection of the action from its evaluation. It is possible to effectively combine this with DQN, using the loss
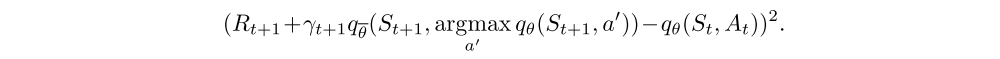
This change was shown to reduce harmful overestimations that were present for DQN, thereby improving performance.
-
Prioritized replay.
DQN samples uniformly from the replay buffer. Ideally, we want to sample more frequently those transitions from which there is much to learn. As a proxy for learning potential, prioritized experience replay samples transitions with probability pt relative to the last encountered absolute TD error:
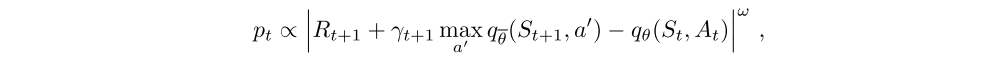
where ω is a hyper-parameter that determines the shape of the distribution. New transitions are inserted into the replay buffer with maximum priority, providing a bias towards recent transitions. Note that stochastic transitions might also be favoured, even when there is little left to learn about them.
-
Dueling networks.
The dueling network is a neural network architecture designed for value based RL. It features two streams of computation, the value and advantage streams, sharing a convolutional encoder, and merged by a special aggregator. This corresponds to the following factorization of action values:
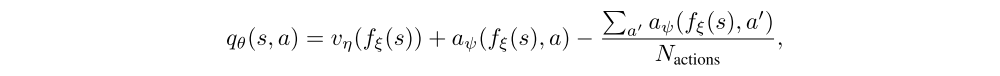
where ξ, η, and ψ are, respectively, the parameters of the shared encoder fξ, of the value stream vη, and of the advantage stream aψ; and θ = {ξ, η, ψ} is their concatenation.
-
Multi-step learning.
Q-learning accumulates a single reward and then uses the greedy action at the next step to bootstrap. Alternatively, forward-view multi-step targets can be used. We define the truncated n-step return from a given state St as
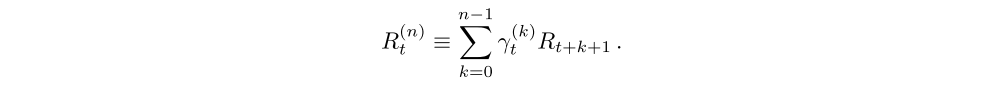
A multi-step variant of DQN is then defined by minimizing the alternative loss,
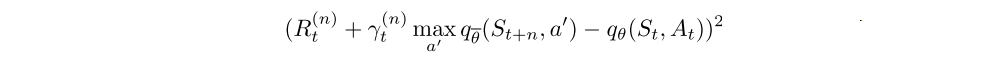
Multi-step targets with suitably tuned n often lead to faster learning.
-
Distributional RL.
We can learn to approximate the distribution of returns instead of the expected return. Recently it was proposed to model such distributions with probability masses placed on a discrete support z, where z is a vector with Natoms ∈ N+ atoms, defined by
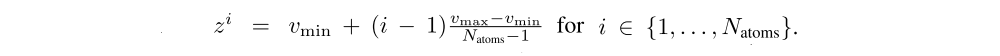
The approximating distribution dt at time t is defined on this support, with the probability mass piθ(St, At) on each atom i, such that dt = (z, pθ(St, At)). The goal is to update θ such that this distribution closely matches the actual distribution of returns.
To learn the probability masses, the key insight is that return distributions satisfy a variant of Bellman’s equation. For a given state St and action At, the distribution of the returns under the optimal policy π∗ should match a target distribution defined by taking the distribution for the next state St+1 and action a∗t+1 = π∗(St+1), contracting it towards zero according to the discount, and shifting it by the reward (or distribution of rewards, in the stochastic case). A distributional variant of Q-learning is then derived by first constructing a new support for the target distribution, and then minimizing the KL divergence between the distribution dt and the target distribution
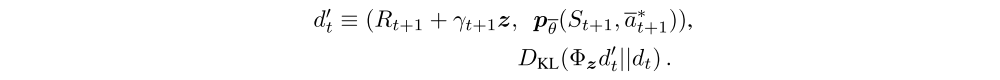
Here Φz is a L2-projection of the target distribution onto the fixed support z, and
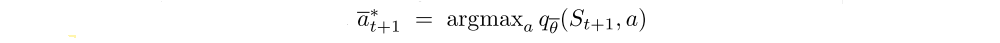
is the greedy action with respect to the mean action values
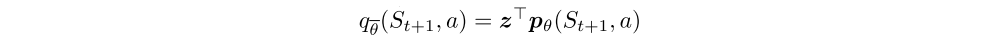
in state St+1.
As in the non-distributional case, we can use a frozen copy of the parameters θ to construct the target distribution. The parametrized distribution can be represented by a neural network, as in DQN, but with Natoms × Nactions outputs. A softmax is applied independently for each action dimension of the output to ensure that the distribution for each action is appropriately normalized.
-
Noisy Nets.
The limitations of exploring using ε-greedy policies are clear in games such as Montezuma’s Revenge, where many actions must be executed to collect the first reward. Noisy Nets propose a noisy linear layer that combines a deterministic and noisy stream,
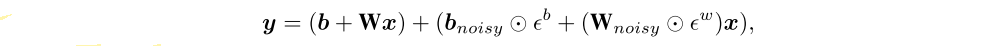
where εb and εw are random variables, and ⊙ denotes the element-wise product. This transformation can then be used in place of the standard linear y = b + Wx. Over time, the network can learn to ignore the noisy stream, but will do so at different rates in different parts of the state space, allowing state-conditional exploration with a form of self-annealing.
4 The Integrated Agent
In this paper we integrate all the aforementioned components into a single integrated agent, which we call Rainbow.
First, we replace the 1-step distributional loss with a multi-step variant. We construct the target distribution by contracting the value distribution in St+n according to the cumulative discount, and shifting it by the truncated n-step discounted return. This corresponds to defining the target distribution as
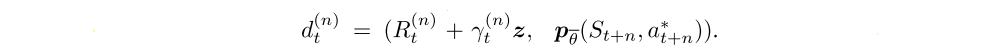
The resulting loss is
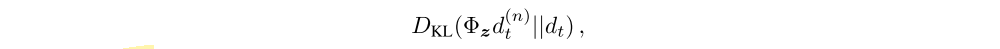
where, again, Φz is the projection onto z.
We combine the multi-step distributional loss with double Q-learning by using the greedy action in St+n selected according to the online network as the bootstrap action a∗t+n, and evaluating such action using the target network.
In standard proportional prioritized replay the absolute TD error is used to prioritize the transitions. This can be computed in the distributional setting, using the mean action values. However, in our experiments all distributional Rainbow variants prioritize transitions by the KL loss, since this is what the algorithm is minimizing:
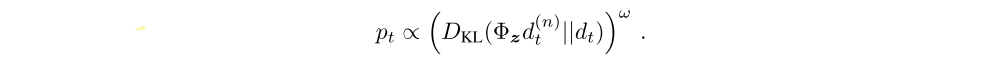
The KL loss as priority might be more robust to noisy stochastic environments because the loss can continue to decrease even when the returns are not deterministic.
The network architecture is a dueling network architecture adapted for use with return distributions. The network has a shared representation fξ(s), which is then fed into a value stream vη with Natoms outputs, and into an advantage stream aξ with Natoms × Nactions outputs, where aiξ(fξ(s), a) will denote the output corresponding to atom i and action a. For each atom zi, the value and advantage streams are aggregated, as in dueling DQN, and then passed through a softmax layer to obtain the normalized parametric distributions used to estimate the returns’ distributions: