Soft Reinforcement Learning（SRL）是强化学习的一个新的范式， 脱胎于最大熵强化学习（Maximum Entropy Reinforcement Learning）， SRL 的 optimal policy 是 soft 的， 即 optimal policy 是 Q-value 的 softmax 函数； 相比之下， 普通的强化学习为 Hard Reinforcement Learning（HRL）， HRL 的 optimal policy 是 hard 的， 即 optimal policy 是 Q-value 的 max 函数。 如果 SRL 中的 α 取为0， 则 SRL 退化成 HRL， 也就是说： HRL 是 SRL 的一个特例。

Berkeley Artificial Intelligence Research Blog

Fisher’s Blog

Abstract

  • We propose a method for learning expressive energy-based policies for continuous states and actions, which has been feasible only in tabular domains before.

  • We apply our method to learning maximum entropy policies, resulting into a new algorithm, called soft Q-learning, that expresses the optimal policy via a Boltzmann distribution. We use the recently proposed amortized Stein variational gradient descent to learn a stochastic sampling network that approximates samples from this distribution.

  • The benefits of the proposed algorithm include improved exploration and compositionality（组合性）that allows transferring skills between tasks, which we confirm in simulated experiments with swimming and walking robots.

  • We also draw a connection to actor-critic methods, which can be viewed performing approximate inference on the corresponding energy-based model.

1 Introduction

In some cases, we might actually prefer to learn stochastic behaviors. In this paper, we explore two potential reasons for this: exploration in the presence of multimodal（多峰的）objectives, and compositionality attained via pretraining. Other benefits include robustness in the face of uncertain dynamics, imitation learning, and improved convergence and computational properties.

In which cases is a stochastic policy actually the optimal solution? As discussed in prior work, a stochastic policy emerges as the optimal answer when we consider the connection between optimal control and probabilistic inference. While there are multiple instantiations of this framework, they typically include the cost or reward function as an additional factor in a factor graph, and infer the optimal conditional distribution over actions conditioned on states. The solution can be shown to optimize an entropy-augmented RL objective or to correspond to the solution to a maximum entropy learning problem. Intuitively, framing control as inference produces policies that aim to capture not only the single deterministic behavior that has the lowest cost, but the entire range of low-cost behaviors, explicitly maximizing the entropy of the corresponding policy. Instead of learning the best way to perform the task, the resulting policies try to learn all of the ways of performing the task. It should now be apparent why such policies might be preferred:

  • if we can learn all of the ways that a given task might be performed, the resulting policy can serve as a good initialization for finetuning to a more specific behavior (e.g. first learning all the ways that a robot could move forward, and then using this as an initialization to learn separate running and bounding skills);

  • a better exploration mechanism for seeking out the best mode in a multi-modal reward landscape;

  • and a more robust behavior in the face of adversarial perturbations, where the ability to perform the same task in multiple different ways can provide the agent with more options to recover from perturbations.

The principal contribution of this work is a tractable, efficient algorithm for optimizing arbitrary multi-modal stochastic policies represented by energy-based models, as well as a discussion that relates this method to other recent algorithms in RL and probabilistic inference.

In our experimental evaluation, we explore two potential applications of our approach.

  1. First, we demonstrate improved exploration performance in tasks with multi-modal reward landscapes, where conventional deterministic or unimodal methods are at high risk of falling into suboptimal local optima.

  2. Second, we explore how our method can be used to provide a degree of compositionality in RL by showing that stochastic energy-based policies can serve as a much better initialization for learning new skills than either random policies or policies pretrained with conventional maximum reward objectives.

2 Preliminaries

In this section, we will define the RL problem that we are addressing and briefly summarize the maximum entropy policy search objective. We will also present a few useful identities that we will build on in our algorithm, which will be presented in Section 3.

2.1 Maximum Entropy Reinforcement Learning

Standard RL objective：


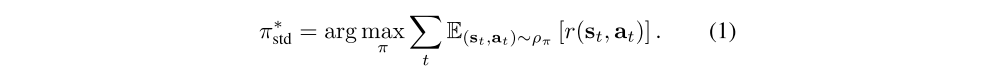
Maximum entropy RL augments the reward with an entropy term, such that the optimal policy aims to maximize its entropy at each visited state:


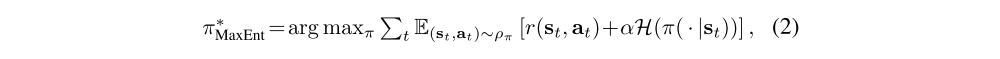
2.2 Soft Value Functions and Energy-Based Models

Optimizing the maximum entropy objective provides us with a framework for training stochastic policies, but we must still choose a representation for these policies. The choices in prior work include discrete multinomial distributions and Gaussian distributions. However, if we want to use a very general class of distributions that can represent complex, multi-modal behaviors, we can instead opt for using general energy-based policies of the form


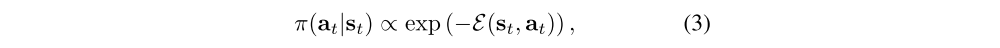
where E is an energy function that could be represented, for example, by a DNN. If we use a universal function approximator for E, we can represent any distribution π(at|st). There is a close connection between such energy-based models and soft versions of value functions and Q-functions, where we set


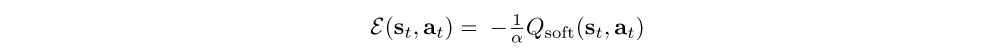
and use the following theorem:


Theorem 1 connects the maximum entropy objective in (2) and energy-based models, where 1/α Qsoft(st, at) acts as the negative energy, and 1/α Vsoft(st) serves as the log-partition function. As with the standard Q-function and value function, we can relate the Q-function to the value function at a future state via a soft Bellman equation:


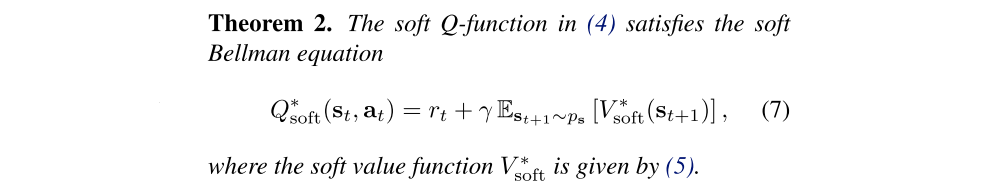
The soft Bellman equation is a generalization of the conventional (hard) equation, where we can recover the more standard equation as α → 0, which causes (5) to approach a hard maximum over the actions. In the next section, we will discuss how we can use these identities to derive a Q-learning style algorithm for learning maximum entropy policies, and how we can make this practical for arbitrary Q-function representations via an approximate inference procedure.

3 Training Expressive Energy-Based Models via Soft Q-Learning

In this section, we will present our proposed RL algorithm, which is based on the soft Q-function described in the previous section, but can be implemented via a tractable SGD procedure with approximate sampling. We will first describe the general case of soft Q-learning, and then present the inference procedure that makes it tractable to use with DNN representations in high-dimensional continuous state and action spaces. In the process, we will relate this Q-learning procedure to inference in energy-based models and actor-critic algorithms.

3.1 Soft Q-Iteration

We can obtain a solution to (7) by iteratively updating estimates of V∗soft and Q∗soft. This leads to a fixed-point iteration that resembles Q-iteration:


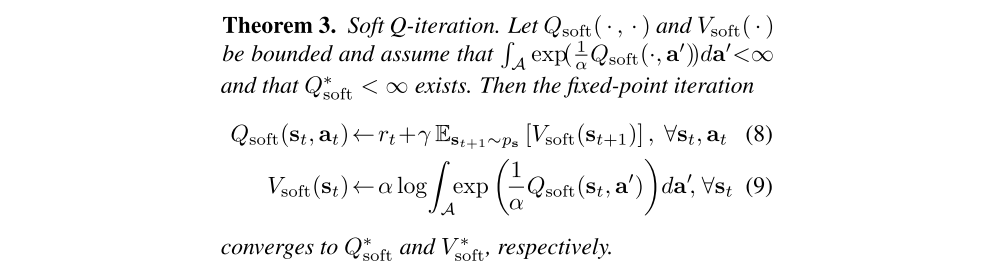
We refer to the updates in (8) and (9) as the soft Bellman backup operator that acts on the soft value function, and denote it by T. The maximum entropy policy in (6) can then be recovered by iteratively applying this operator until convergence. However, there are several practicalities that need to be considered in order to make use of the algorithm.

  1. First, the soft Bellman backup cannot be performed exactly in continuous or large state and action spaces,

  2. Second, sampling from the energy-based model in (6) is intractable in general.

We will address these challenges in the following sections.

3.2 Soft Q-Learning

This section discusses how the Bellman backup in Theorem 3 can be implemented in a practical algorithm that uses a finite set of samples from the environment, resulting in a method similar to Q-learning. Since the soft Bellman backup is a contraction, the optimal value function is the fixed point of the Bellman backup, and we can find it by optimizing for a Q-function for which the soft Bellman error |TQ − Q| is minimized at all states and actions. While this procedure is still intractable due to the integral（积分）in (9) and the infinite set of all states and actions, we can express it as a stochastic optimization, which leads to a SGD update procedure. We will model the soft Q-function with a function approximator with parameters θ and denote it as Qθsoft(st, at).

To convert Theorem 3 into a stochastic optimization problem, we first express the soft value function in terms of an expectation via importance sampling:


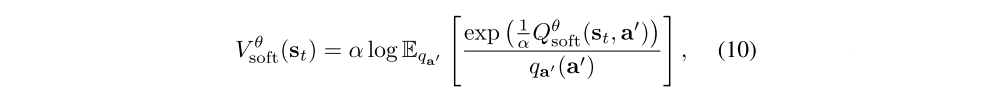
where qa’ can be an arbitrary distribution over the action space. Second, by noting the identity


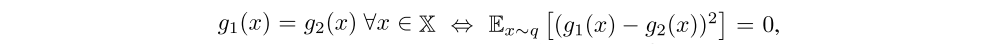
where q can be any strictly positive density function on X, we can express the soft Q-iteration in an equivalent form as minimizing


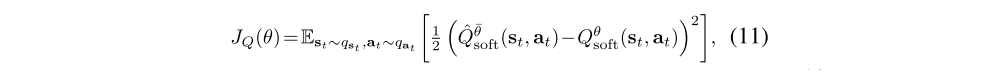
where qst, qat are positive over S and A respectively,


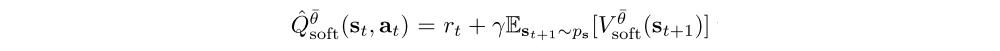
is a target Q-value, with Vθ¯soft(st+1) given by (10) and θ being replaced by the target parameters, θ¯.

This stochastic optimization problem can be solved approximately using SGD using sampled states and actions. While the sampling distributions qst and qat can be arbitrary, we typically use real samples from rollouts of the current policy


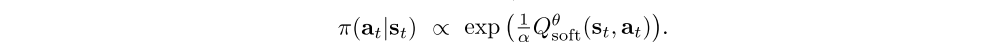
For qa’ we have more options. A convenient choice is a uniform distribution. However, this choice can scale poorly to high dimensions. A better choice is to use the current policy, which produces an unbiased estimate of the soft value as can be confirmed by substitution. This overall procedure yields an iterative approach that optimizes over the Q-values, which we summarize in Section 3.4.

However, in continuous spaces, we still need a tractable way to sample from the policy above, both to take on-policy actions and, if so desired, to generate action samples for estimating the soft value function. Since the form of the policy is so general, sampling from it is intractable. We will therefore use an approximate sampling procedure, as discussed in the following section.

3.3 Approximate Sampling and Stein Variational Gradient Descent (SVGD)

In this section we describe how we can approximately sample from the soft Q-function. Existing approaches that sample from energy-based distributions generally fall into two categories: methods that use Markov chain Monte Carlo (MCMC) based sampling, and methods that learn a stochastic sampling network trained to output approximate samples from the target distribution. Since sampling via MCMC is not tractable when the inference must be performed online, we will use a sampling network based on Stein variational gradient descent (SVGD) and amortized SVGD. Amortized SVGD has several intriguing properties:

  1. First, it provides us with a stochastic sampling network that we can query for extremely fast sample generation.

  2. Second, it can be shown to converge to an accurate estimate of the posterior distribution of an EBM.

  3. Third, the resulting algorithm, as we will show later, strongly resembles actor-critic algorithm, which provides for a simple and computationally efficient implementation and sheds light on the connection between our algorithm and prior actor-critic methods.

Formally, we want to learn a state-conditioned stochastic neural network at = fφ(ξ; st), parametrized by φ, that maps noise samples ξ drawn from a normal Gaussian, or other arbitrary distribution, into unbiased action samples from the target EBM corresponding to Qθsoft. We denote the induced distribution of the actions as πφ(at|st), and we want to find parameters φ so that the induced distribution approximates the energy-based distribution in terms of the KL divergence


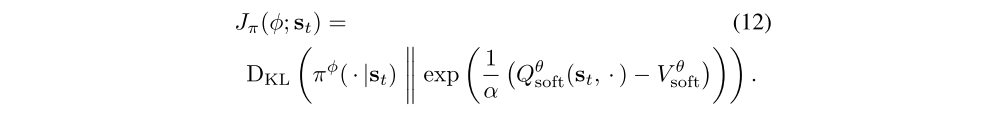
Suppose we “perturb” a set of independent samples a(i)t = fφ(ξ(i); st) in appropriate directions ∆fφ(ξ(i); st), the induced KL divergence can be reduced. SVGD provides the most greedy directions as a functional


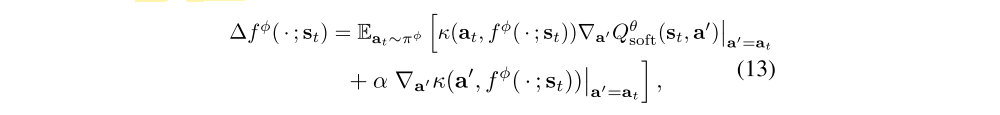
where κ is a kernel function (typically Gaussian, see details in Appendix). To be precise, ∆fφ is the optimal direction in the reproducing kernel Hilbert space of κ, and is thus not strictly speaking the gradient of (12), but it turns out that we can set ∂Jπ/∂at ∝ ∆fφ as explained in prior work. With this assumption, we can use the chain rule and backpropagate the Stein variational gradient into the policy network according to


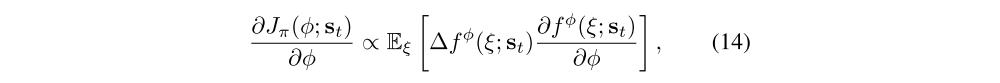
and use any gradient-based optimization method to learn the optimal sampling network parameters. The sampling network fφ can be viewed as an actor in an actor-critic algorithm. We will discuss this connection in Section 4, but first we will summarize our complete maximum entropy policy learning algorithm.

3.4 Algorithm Summary

To summarize, we propose the soft Q-learning algorithm for learning maximum entropy policies in continuous domains. The algorithm proceeds by alternating between collecting new experience from the environment, and updating the soft Q-function and sampling network parameters. The experience is stored in a replay memory buffer D as standard in DQN2013, and the parameters are updated using random mini-batches from this memory. The soft Q-function updates use a delayed version of the target values. For optimization, we use the ADAM optimizer and empirical estimates of the gradients, which we denote by ∇ˆ. The exact formulate used to compute the gradient estimates is deferred to Appendix C, which also discusses other implementation details, but we summarize an overview of soft Q-learning in Algorithm 1.