Introduction


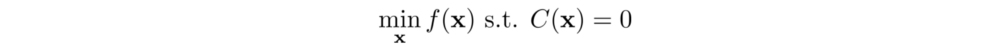
The key idea is transforming the objective into a Lagrange dual function which can be optimized iteratively. The Lagrangian 饾摏 and the Lagrange dual function g is defined as:


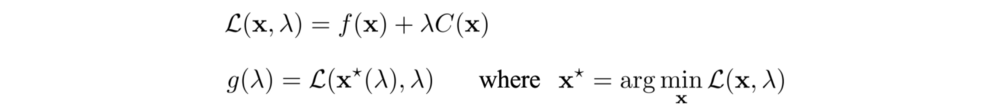
where 位 is a scalar which we call the Lagrangian multiplier.

The dual function g is a lower bound for the original optimization problem. Indeed, if the function f is a convex function, the strong duality will often hold which say the maximum value of g equals the minimum values of the optimization problem. Hence, if we find 位 that maximize g, we solve the optimization problem.

So we start with a random guess of 位 and use any optimization method to solve this unconstrained objective.


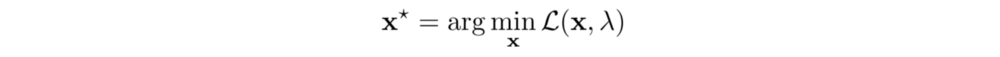
Next, we will apply gradient ascent to update 位 in order to maximize g. The gradient of g is:


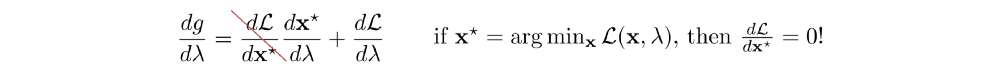
i.e.


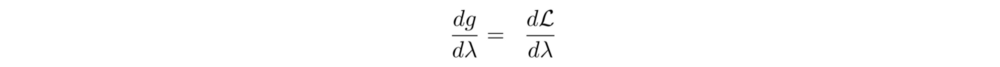
In step 1 below, we find the minimum x based on the current 位 value, and then we take a gradient ascent step for g (step 2 and 3).


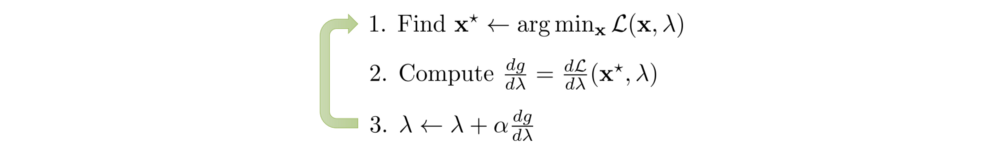
We alternate between minimizing the Lagrangian 饾摏 with respect to the primal variables x, and incrementing the Lagrange multiplier 位 by its gradient. By repeating the iteration, the solution will converge.

Visualization


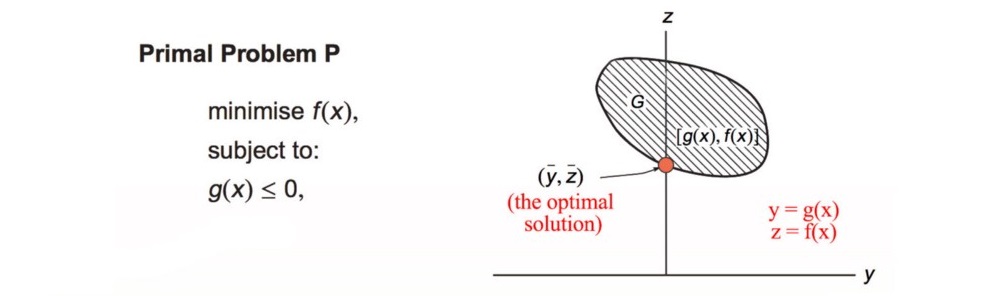
Let y = g(x) and z = f(x). y and z form a space G above and we plot z against y. Our solution is the orange dot above: the minimum f within the space G and g(x) = 0. The orange line below is our Lagrangian. Its slope equals 位 and it touches the boundary of G.


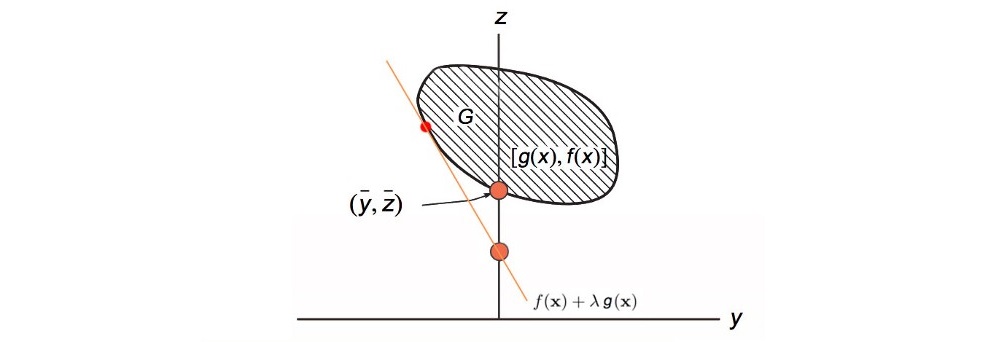
Then we use gradient ascent to adjust 位 (the slope) for the maximum value f(x) that touches G with g(x) = 0.


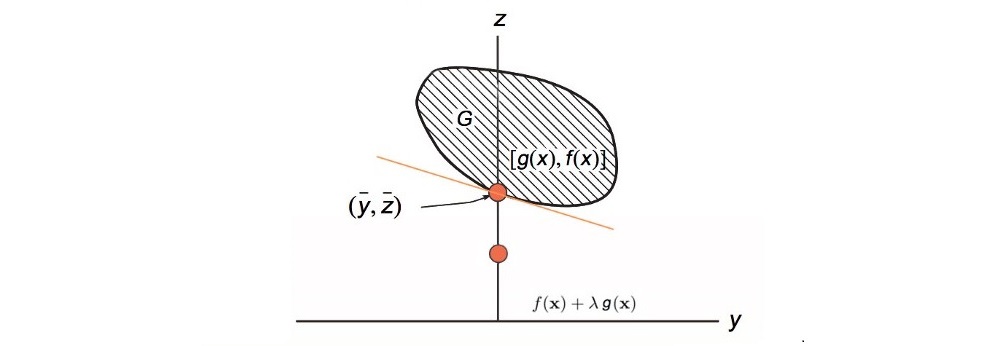
Lagrange Multiplier

So what is this Lagrange multiplier? We can visualize f with a contour plot with different values of d. g is the constraint function.


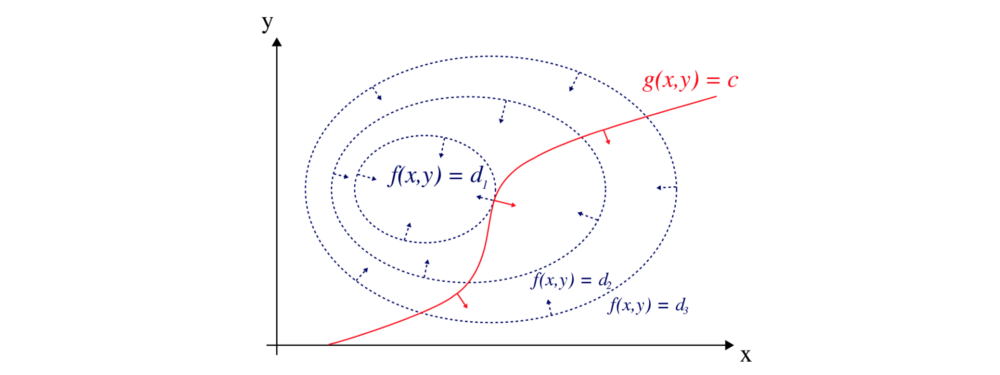
Geometrically, the optimal point lies where the gradient at f(x, y), the blue arrow, aligned with the gradient at g(x, y), the red arrow.


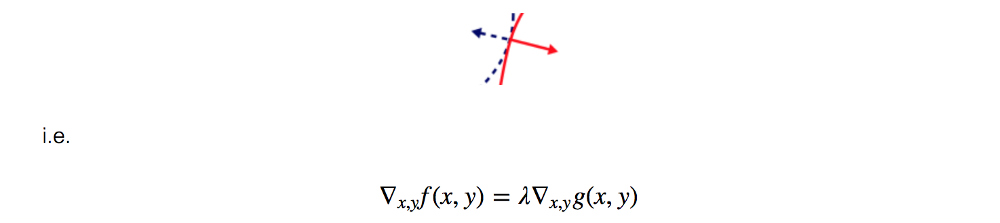
where 位 is the Lagrange multiplier.