Soft Actor-Critic 共经历了三个连续的版本

  • 在前两个版本中， 除了 action-value function 网络之外还使用了 value function 网络，

  • 第二个版本借鉴了来自 TD3 的 double critic trick，

  • 这里介绍的第三个版本移除了 value function 网络 （实际作用不明显）， 并且使用了正则项。

OpenAI Spinning Up

Abstract

  • Model-free DRL algorithms typically suffer from two major challenges: high sample complexity and brittleness to hyperparameters.

  • In this paper, we describe Soft Actor-Critic (SAC), our recently introduced off-policy actor-critic algorithm based on the maximum entropy RL framework.

  • In this framework, the actor aims to simultaneously maximize expected return and entropy; that is, to succeed at the task while acting as randomly as possible. We extend SAC to incorporate a number of modifications that accelerate training and improve stability with respect to the hyperparameters, including a constrained formulation that automatically tunes the temperature hyperparameter.

1 Introduction

In Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor, we introduced the SAC algorithm based on the maximum entropy framework. In the first sections of this paper, we summarize the SAC algorithm, describe the reasoning behind the design choices, and present key theoretical results from the previous version. Unfortunately, SAC as presented in the previous version can suffer from brittleness to the temperature hyperparameter. Unlike in conventional RL, where the optimal policy is independent of scaling of the reward function, in maximum entropy RL the scaling factor has to be compensated（补偿）by the choice a of suitable temperature, and a sub-optimal temperature can drastically degrade performance.

To resolve this issue, we devise an automatic gradient-based temperature tuning method that adjusts the expected entropy over the visited states to match a target value. Although this modification is technically simple, we find that in practice it largely eliminates the need for per-task hyperparameter tuning.

Finally, we present empirical results that show that SAC attains a substantial improvement in both performance and sample efficiency over prior off-policy and on-policy methods including the recently introduced twin delayed deep deterministic (TD3) policy gradient algorithm. We also evaluate our method on real-world challenging tasks such as locomotion for a quadrupedal robot and robotic manipulation with a dexterous hand from image observations.

Maximum entropy RL generalizes the expected return RL objective, although the original objective can be recovered in the zero temperature limit. More importantly, the maximum entropy formulation provides a substantial improvement in exploration and robustness: maximum entropy policies are robust in the face of model and estimation errors, and they improve exploration by acquiring diverse behaviors.

Our soft actor-critic algorithm incorporates three key ingredients: an actor-critic architecture with separate policy and value function networks, an off-policy formulation that enables reuse of previously collected data for efficiency, and entropy maximization to encourage stability and exploration.

Actor-critic algorithms are typically derived starting from policy iteration, which alternates between policy evaluation—computing the value function for a policy—and policy improvement—using the value function to obtain a better policy. In large-scale RL problems, it is typically impractical to run either of these steps to convergence, and instead the value function and policy are optimized jointly. In this case, the policy is referred to as the actor, and the value function as the critic. Many actor-critic algorithms build on the standard, on-policy policy gradient formulation to update the actor, and many of them also consider the entropy of the policy, but instead of maximizing the entropy, they use it as an regularizer. On-policy training tends to improve stability but results in poor sample complexity.

3 Preliminaries

3.2 Maximum Entropy Reinforcement Learning

The maximum entropy objective generalizes the standard objective by augmenting it with an entropy term, such that the optimal policy additionally aims to maximize its entropy at each visited state:


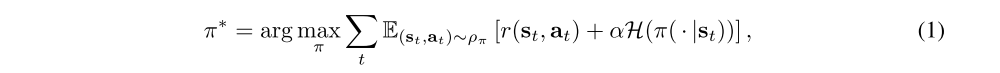
where α is the temperature parameter that determines the relative importance of the entropy term versus the reward, and thus controls the stochasticity of the optimal policy. Although the maximum entropy objective differs from the standard maximum expected return objective used in conventional RL, the conventional objective can be recovered in the limit as α → 0. If we wish to extend either the conventional or the maximum entropy RL objective to infinite horizon problems, it is convenient to also introduce a discount factor γ to ensure that the sum of expected rewards (and entropies) is finite.

The maximum entropy objective has a number of conceptual and practical advantages.

  • First, the policy is incentivized to explore more widely, while giving up on clearly unpromising avenues.

  • Second, the policy can capture multiple modes of near-optimal behavior. In problem settings where multiple actions seem equally attractive, the policy will commit equal probability mass to those actions.

  • In practice, we observe improved exploration with this objective, as also has been reported in the prior work, and we observe that it considerably improves learning speed over SOTA methods that optimize the conventional RL objective function.

Our method is, to our knowledge, the first off-policy actor-critic method in the maximum entropy RL framework.

4 From Soft Policy Iteration to Soft Actor-Critic

Our off-policy soft actor-critic algorithm can be derived starting from a maximum entropy variant of the policy iteration method.

  1. We will first present this derivation, verify that the corresponding algorithm converges to the optimal policy from its density class,

  2. and then present a practical DRL algorithm based on this theory.

  3. In this section, we treat the temperature as a constant, and later in Section 5 propose an extension to SAC that adjusts the temperature automatically to match an entropy target in expectation.

4.1 Soft Policy Iteration

We will begin by deriving soft policy iteration, a general algorithm for learning optimal maximum entropy policies that alternates between policy evaluation and policy improvement in the maximum entropy framework. Our derivation is based on a tabular setting, to enable theoretical analysis and convergence guarantees, and we extend this method into the general continuous setting in the next section. We will show that soft policy iteration converges to the optimal policy within a set of policies which might correspond, for instance, to a set of parameterized densities.

In the policy evaluation step of soft policy iteration, we wish to compute the value of a policy π according to the maximum entropy objective. For a fixed policy, the soft Q-value can be computed iteratively, starting from any function Q: S × A → R and repeatedly applying a modified Bellman backup operator Tπ given by


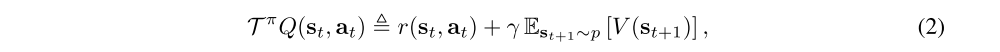
where


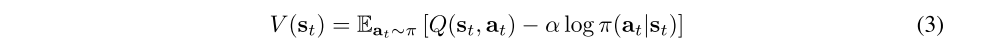
is the soft state value function. We can obtain the soft Q-function for any policy π by repeatedly applying Tπ as formalized below.


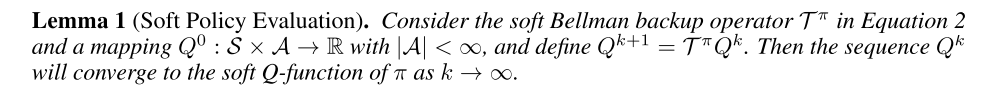
In the policy improvement step, we update the policy towards the exponential of the new soft Q-function. This particular choice of update can be guaranteed to result in an improved policy in terms of its soft value. Since in practice we prefer policies that are tractable, we will additionally restrict the policy to some set of policies Π, which can correspond, for example, to a parameterized family of distributions such as Gaussians. To account for the constraint that π ∈ Π, we project the improved policy into the desired set of policies. While in principle we could choose any projection, it will turn out to be convenient to use the information projection defined in terms of the Kullback-Leibler divergence. In the other words, in the policy improvement step, for each state, we update the policy according to


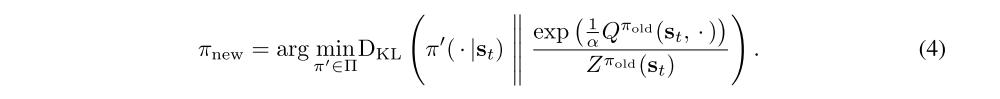
The partition function Zπold(st) normalizes the distribution, and while it is intractable in general, it does not contribute to the gradient with respect to the new policy and can thus be ignored. For this projection, we can show that the new, projected policy has a higher value than the old policy with respect to the maximum entropy objective. We formalize this result in Lemma 2


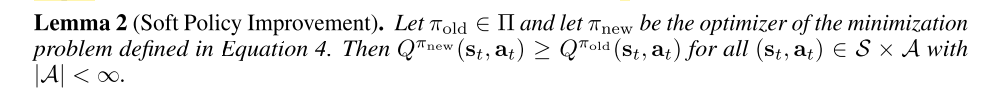
The full soft policy iteration algorithm alternates between the soft policy evaluation and the soft policy improvement steps, and it will provably converge to the optimal maximum entropy policy among the policies in Π (Theorem 1). Although this algorithm will provably find the optimal solution, we can perform it in its exact form only in the tabular case. Therefore, we will next approximate the algorithm for continuous domains, where we need to rely on a function approximator to represent the Q-values, and running the two steps until convergence would be computationally too expensive. The approximation gives rise to a new practical algorithm, called soft actor-critic.


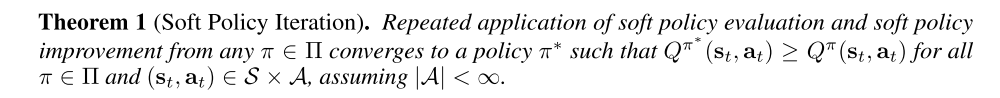
4.2 Soft Actor-Critic

As discussed above, large continuous domains require us to derive a practical approximation to soft policy iteration. To that end, we will use function approximators for both the soft Q-function and the policy, and instead of running evaluation and improvement to convergence, alternate between optimizing both networks with stochastic gradient descent. We will consider a parameterized soft Q-function Qθ(st, at) and a tractable policy πφ(at|st). The parameters of these networks are θ and φ. For example, the soft Q-function can be modeled as expressive neural networks, and the policy as a Gaussian with mean and covariance given by neural networks. We will next derive update rules for these parameter vectors.

The soft Q-function parameters can be trained to minimize the soft Bellman residual


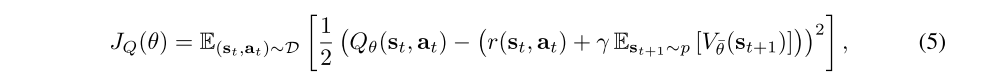
where the value function is implicitly parameterized through the soft Q-function parameters via Equation 3, and it can be optimized with stochastic gradients


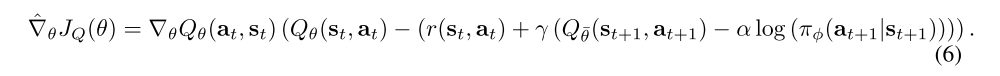
The update makes use of a target soft Q-function with parameters θ¯ that are obtained as an exponentially moving average of the soft Q-function weights, which has been shown to stabilize training. Finally, the policy parameters can be learned by directly minimizing the expected KL-divergence in Equation 4 (multiplied by α and ignoring the constant log-partition function and by α):


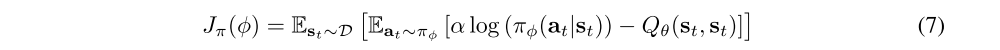
There are several options for minimizing Jπ. A typical solution for policy gradient methods is to use the likelihood ratio gradient estimator, which does not require backpropagating the gradient through the policy and the target density networks. However, in our case, the target density is the Q-function, which is represented by a neural network an can be differentiated, and it is thus convenient to apply the reparameterization trick instead, resulting in a lower variance estimator. To that end, we reparameterize the policy using a neural network transformation


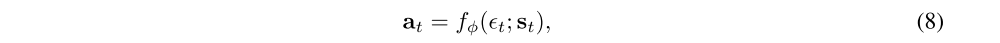
where εt is an input noise vector, sampled from some fixed distribution, such as a spherical Gaussian. We can now rewrite the objective in Equation 7 as


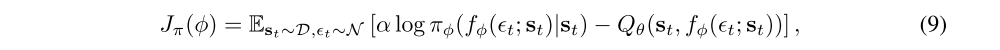
where πφ is defined implicitly in terms of fφ. We can approximate the gradient of Equation 9 with


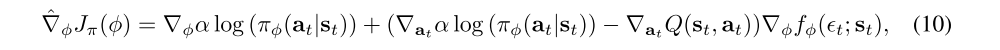
where at is evaluated at fφ(εt; st). This unbiased gradient estimator extends the DDPG style policy gradients to any tractable stochastic policy.

5 Automating Entropy Adjustment for Maximum Entropy RL

In the previous section, we derived a practical off-policy algorithm for learning maximum entropy policies of a given temperature. Unfortunately, choosing the optimal temperature is non-trivial, and the temperature needs to be tuned for each task. Instead of requiring the user to set the temperature manually, we can automate this process by formulating a different maximum entropy RL objective, where the entropy is treated as a constraint. The magnitude of the reward differs not only across tasks, but it also depends on the policy, which improves over time during training. Since the optimal entropy depends on this magnitude, this makes the temperature adjustment particularly difficult: the entropy can vary unpredictably both across tasks and during training as the policy becomes better. Simply forcing the entropy to a fixed value is a poor solution, since the policy should be free to explore more in regions where the optimal action is uncertain, but remain more deterministic in states with a clear distinction between good and bad actions. Instead, we formulate a constrained optimization problem where the average entropy of the policy is constrained, while the entropy at different states can vary. Similar approach was taken in prior work, where the policy was constrained to remain close to the previous policy. We show that the dual to this constrained optimization leads to the soft actor-critic updates, along with an additional update for the dual variable, which plays the role of the temperature. Our formulation also makes it possible to learn the entropy with more expressive policies that can model multi-modal distributions, such as policies based on normalizing flows for which no closed form expression for the entropy exists. We will derive the update for finite horizon case, and then derive an approximation for stationary policies by dropping the time dependencies from the policy, soft Q-function, and the temperature.

Our aim is to find a stochastic policy with maximal expected return that satisfies a minimum expected entropy constraint. Formally, we want to solve the constrained optimization problem


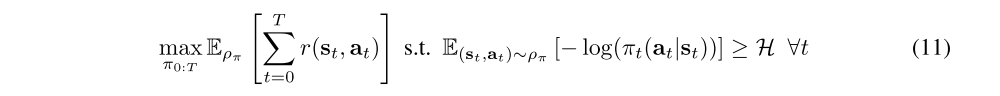
where H is a desired minimum expected entropy. Note that, for fully observed MDPs, the policy that optimizes the expected return is deterministic, so we expect this constraint to usually be tight and do not need to impose an upper bound on the entropy.

对于该部分内容，这篇博客有极其清晰的介绍。

6 Practical Algorithm

Our algorithm makes use of two soft Q-functions to mitigate positive bias in the policy improvement step that is known to degrade performance of value based methods. In particular, we parameterize two soft Q-functions, with parameters θi, and train them independently to optimize JQ(θi). We then use the minimum of the the soft Q-functions for the stochastic gradient in Equation 6 and policy gradient in Equation 10. Although our algorithm can learn challenging tasks, including a 21-dimensional Humanoid, using just a single Q-function, we found two soft Q-functions significantly speed up training, especially on harder tasks.

In addition to the soft Q-function and the policy, we also learn α by minimizing the dual objective. This can be done by approximating dual gradient descent. Dual gradient descent alternates between optimizing the Lagrangian with respect to the primal variables to convergence, and then taking a gradient step on the dual variables. While optimizing with respect to the primal variables fully is impractical, a truncated version that performs incomplete optimization (even for a single gradient step) can be shown to converge under convexity assumptions. While such assumptions do not apply to the case of nonlinear function approximators such as neural networks, we found this approach to still work in practice. Thus, we compute gradients for α with the following objective:


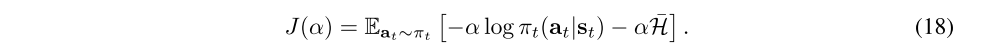
The final algorithm is listed in Algorithm 1. The method alternates between collecting experience from the environment with the current policy and updating the function approximators using the stochastic gradients from batches sampled from a replay pool. Using off-policy data from a replay pool is feasible because both value estimators and the policy can be trained entirely on off-policy data. The algorithm is agnostic to the parameterization of the policy, as long as it can be evaluated for any arbitrary state-action tuple.